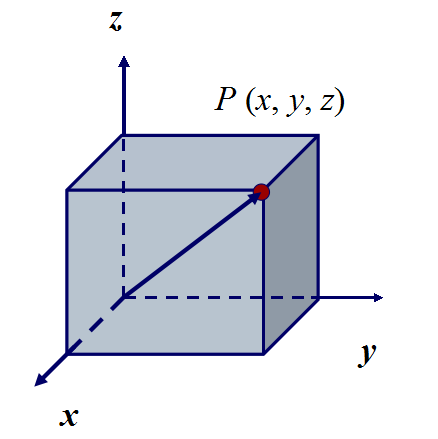
-
坐标系 编辑
坐标系,是理科常用辅助方法,常见有直线坐标系,平面直角坐标系。为了说明质点的位置、运动的快慢、方向等,必须选取其坐标系。在参照系中,为确定空间一点的位置,按规定方法选取的有次序的一组数据,这就叫做“坐标”。在某一问题中规定坐标的方法,就是该问题所用的坐标系。坐标系的种类很多,常用的坐标系有:笛卡尔直角坐标系、平面极坐标系、柱面坐标系(或称柱坐标系)和球面坐标系(或称球坐标系)等。中学物理学中常用的坐标系,为直角坐标系,或称为正交坐标系。从广义上讲:事物的一切抽象概念都是参照于其所属的坐标系存在的,同一个事物在不同的坐标系中就会有不同抽象概念来表示,坐标系表达的事物有联系的抽象概念的数量【既坐标轴的数量】就是该事物所处空间的维度。两件能相互改变的事物必须在同坐标系中。
坐标系可分为:
直线坐标系:物体在一条直线上运动,只需建立直线坐标系。
平面直角坐标系:物体在某一平面内运动。
 百科x混知:图解笛卡尔
百科x混知:图解笛卡尔
蜘蛛的“表演”,使笛卡尔思路豁然开朗。他想,可以把蜘蛛看做一个点,它在屋子里可以上、下、左、右运动,能不能把蜘蛛的每个位置用一组数确定下来呢?他又想,屋子里相邻的两面墙与地面交出了三条线,如果把地面上的墙角作为起点,把交出来的三条线作为三根数轴,那么空间中任意一点的位置,不是都可以用这三根数轴上找到的有顺序的三个数来表示吗?反过来,任意给一组三个有顺序的数,例如3.2.1,也可以用空间中的一个点 P来表示它们(如图 1)。同样,用一组数(a, b)可以表示平面上的一个点,平面上的一个点也可以用一组二个有顺序的数来表示(如图2)。于是在蜘蛛的启示下,笛卡尔创建了直角坐标系。
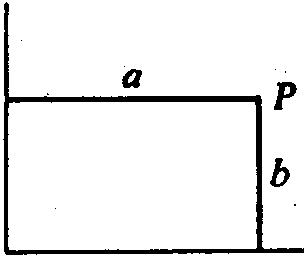 图2
图2
直角坐标系的创建,在代数和几何上架起了一座桥梁。它使几何概念得以用代数的方法来描述,几何图形可以通过代数形式来表达,这样便可将先进的代数方法应用于几何学的研究。
笛卡尔在创建直角坐标系的基础上,创造了用代数方法来研究几何图形的数学分支——解析几何。他的设想是:只要把几何图形看成是动点的运动轨迹,就可以把几何图形看成是由具有某种共同特性的点组成的。比如,我们把圆看成是一个动点对定点O作等距离运动的轨迹,也就可以把圆看作是由无数到定点O的距离相等的点组成的。我们把点看作是组成图形的基本元素,把数看成是组成方程的基本元素,只要把点和数挂上钩,也就可以把几何和代数挂上钩。
 坐标系
坐标系
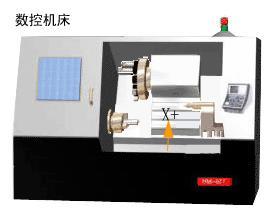
如果机床上有几个主轴,则选一个垂直于工件装夹平面的主轴方向为Z坐标方向;如果主轴能够摆动,则选垂直于工件装夹平面的方向为Z坐标方向;如果机床无主轴,则选垂直于工件装夹平面的方向为Z坐标方向。图3 所示为数控车床的Z坐标。
2.X坐标
X坐标平行于工件的装夹平面,一般在水平面内。
如果工件做旋转运动,则刀具离开工件的方向为X坐标的正方向;
如果刀具做旋转运动,则分为两种情况:
1)Z坐标水平时,观察者沿刀具主轴向工件看时,+X运动方向指向右方;
2)Z坐标垂直时,观察者面对刀具主轴向立柱看时,+X运动方向指向右方。
图4所示为数控车床的X坐标。
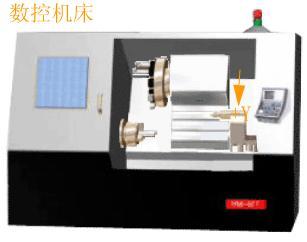
3.Y坐标
 坐标系
坐标系
图5所示为数控车床的Y坐标。
根据图4所示的数控立式铣床结构图,试确定X、Y、Z直线坐标。
(1)Z坐标:平行于主轴,刀具离开工件的方向为正。
(2)X坐标:Z坐标垂直,且刀具旋转,所以面对刀具主轴向立柱方向看,向右为正。
(3)Y坐标:在Z、X坐标确定后,用右手直角坐标系来确定。
 坐标系
坐标系
恩格斯高度评价笛卡尔的工作,他说:“数学中的转折点是笛卡尔的变数。有了变数,运动进入了数学,有了变数,辩证法进入了数学。”
坐标方法在日常生活中用得很多。例如象棋、国际象棋中棋子的定位;电影院、剧院、体育馆的看台、火车车厢的座位及高层建筑的房间编号等都用到坐标的概念。
随着同学们知识的不断增加,坐标方法的应用会更加广泛。
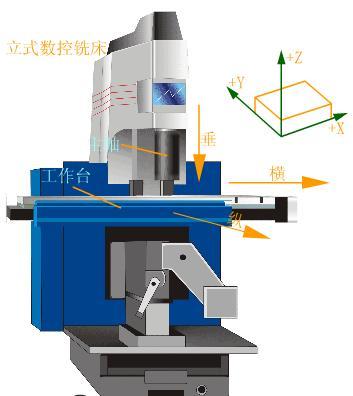
机床
1.机床相对运动的规定
 坐标系
坐标系
2.机床坐标系的规定
在数控机床上,机床的动作是由数控装置来控制的,为了确定数控机床上的成形运动和辅助运动,必须先确定机床上运动的位移和运动的方向,这就需要通过坐标系来实现,这个坐标系被称之为机床坐标系。
例如铣床上,有机床的纵向运动、横向运动以及垂向运动,如图1所示。在数控加工中就应该用机床坐标系来描述,如图2所示。请按图2中按钮观察机床坐标系的相互关系。
 坐标系
坐标系
2)大拇指的指向为X坐标的正方向,食指的指向为Y坐标的正方向,中指的指向为Z坐标的正方向。
3)围绕X、Y、Z坐标旋转的旋转坐标分别用A、B、C表示,根据右手螺旋定则,大拇指的指向为X、Y、Z坐标中任意一轴的正向,则其余四指的旋转方向即为旋转坐标A、B、C的正向。
请按图3中按钮观察机床运动的方向
(3)运动方向的规定
增大刀具与工件距离的方向即为各坐标轴的正方向。
编程
编程坐标系编程人员根据零件图样及加工工艺等建立的坐标系。
编程坐标系一般供编程使用,确定编程坐标系时不必考虑工件毛坯在机床上的实际装夹位置。如图6所示。
编程原点是根据加工零件图样及加工工艺要求选定的编程坐标系的原点。
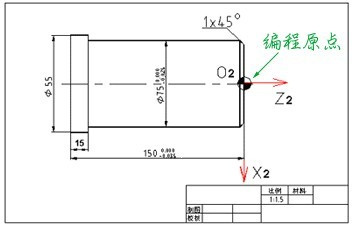
编程原点应尽量选择在零件的设计基准或工艺基准上,编程坐标系中各轴的方向应该与所使用的数控机床相应的坐标轴方向一致,如图7所示为车削零件的编程原点。
加工
1.加工坐标系的确定
加工坐标系是指以确定的加工原点为基准所建立的坐标系。
 坐标系
坐标系
在加工过程中,数控机床是按照工件装夹好后所确定的加工原点位置和程序要求进行加工的。编程人员在编制程序时,只要根据零件图样就可以选定编程原点、建立编程坐标系、计算坐标数值,而不必考虑工件毛坯装夹的实际位置。
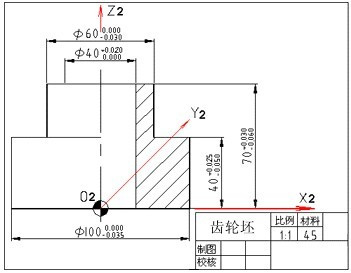
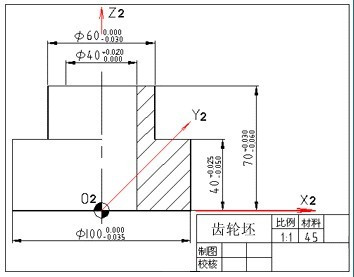
对于加工人员来说,则应在装夹工件、调试程序时,将编程原点转换为加工原点,并确定加工原点的位置,在数控系统中给予设定(即给出原点设定值),设定加工坐标系后就可根据刀具当前位置,确定刀具起始点的坐标值。在加工时,工件各尺寸的坐标值都是相对于加工原点而言的,这样数控机床才能按照准确的加工坐标系位置开始加工。图8中O2为编程原点。
2.加工坐标系的设定
方法一:在机床坐标系中直接设定加工原点。
(1)加工坐标系的选择
编程原点设置在工件轴心线与工件底端面的交点上。
 坐标系
坐标系
(2)设定加工坐标系指令
1)G54~G59为设定加工坐标系指令。G54对应一号工件坐标系,其余以此类推。可在MDI 方式的参数设置页面中,设定加工坐标系。如对已选定的加工原点O3,将其坐标值
X3= -345.700mm
Y3= -196.220mm
Z3=-53.165mm
设在G54中,如图10所示。则表明在数控系统中设定了一号工件加工坐标。设置页面如图10。
2)G54~G59在加工程序中出现时,即选择了相应的加工坐标系。
方法二:通过刀具起始点来设定加工坐标系。
(1)加工坐标系的选择
加工坐标系的原点可设定在相对于刀具起始点的某一符合加工要求的空间点上。
应注意的是,当机床开机回参考点之后,无论刀具运动到哪一点,数控系统对其位置都是已知的。也就是说,刀具起始点是一个已知点。
(2)设定加工坐标系指令
 坐标系
坐标系
该程序段运行后,就根据刀具起始点设定了加工原点,如图11所示。
从图11中可看出,用G92设置加工坐标系,也可看作是:在加工坐标系中,确定刀具起始点的坐标值,并将该坐标值写入G92编程格式中。
例题:在图5中,当a=50mm,b=50mm,c=10mm时,试用G92指令设定加工坐标系。
设定程序段为 G92 X50 Y50 Z10。
机床加工
1.数控铣床(FANUC 0M)加工坐标系的设定步骤
 坐标系
坐标系
(1)准备工作
机床回参考点,确认机床坐标系;
(2)装夹工件毛坯
通过夹具使零件定位,并使工件定位基准面与机床运动方向一致;
(3)对刀测量
用简易对刀法测量,方法如下:
用直径为φ10的标准测量棒、塞尺对刀,得到测量值为X = -437.726, Y = -298.160,如图2所示。Z = -31.833,如图13所示。
(4)计算设定值
将前面已测得的各项数据,按设定要求运算。
X坐标设定值:X= -437.726+5+0.1+40= -392.626mm
注:如图13所示。
-437.726mm为X坐标显示值;
+5mm为测量棒半径值;
+0.1mm为塞尺厚度;
+40.0为编程原点到工件定位基准面在X坐标方向的距离。
Y坐标设定值:Y= -298.160+5+0.1+46.5= -246.46mm
 坐标系
坐标系
注:-31.833为坐标显示值;-0.2为塞尺厚度,如图3所示。
通过计算结果为:X -392.626;Y -246.460;Z -32.033
(5)设定加工坐标系
将开关放在 MDI 方式下,进入加工坐标系设定页面。输入数据为:
X= -392.626 Y= -246.460 Z= -32.033
表示加工原点设置在机床坐标系的X= -392.626 Y= -246.460 Z= -32.033 的位置上。
(6)校对设定值
对于初学者,在进行了加工原点的设定后,应进一步校对设定值,以保证参数的正确性。
校对工作的具体过程如下:在设定了G54加工坐标系后,再进行回机床参考点操作,其显示值为
X +392.626
Y +246.460
Z +32.033
这说明在设定了G54加工坐标系后,机床原点在加工坐标系中的位置为:
X +392.626
Y +246.460
Z +32.033
这反过来也说明G54的设定值是正确的。
2.注意事项
(1)G54~G59设置加工坐标系的方法是一样的,但在实际情况下,机床厂家为了用户的不同需要,在使用中有以下区别:利用G54设置机床原点的情况下,进行回参考点操作时机床坐标值显示为G54的设定值,且符号均为正;利用G55~G59设置加工坐标系的情况下,进行回参考点操作时机床坐标值显示零值。
(2)G92指令与G54~G59指令都是用于设定工件加工坐标系的,但在使用中是有区别的。G92指令是通过程序来设定、选用加工坐标系的,它所设定的加工坐标系原点与当前刀具所在的位置有关,这一加工原点在机床坐标系中的位置是随当前刀具位置的不同而改变的。
(3)G54~G59指令是通过MDI在设置参数方式下设定工件加工坐标系的,一旦设定,加工原点在机床坐标系中的位置是不变的,它与刀具的当前位置无关,除非再通过MDI 方式修改。
(4)本课程所例加工坐标系的设置方法,仅是FANUC系统中常用的方法之一,其余不一一例举。其它数控系统的设置方法应按随机说明书执行。
3.常见错误
当执行程序段G92 X 10 Y 10时,常会认为是刀具在运行程序后到达X 10 Y 10 点上。其实, G92指令程序段只是设定加工坐标系,并不产生任何动作,这时刀具已在加工坐标系中的 X10 Y10点上。
G54~G59指令程序段可以和G00、G01指令组合,如G54 G90 G01 X 10 Y10时,运动部件在选定的加工坐标系中进行移动。 程序段运行后,无论刀具当前点在哪里,它都会移动到加工坐标系中的X 10 Y 10 点上。
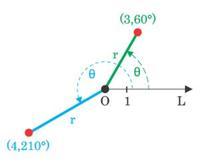
极坐标系
 极坐标系
极坐标系
极点的极径为零 ,极角任意。若除去上述限制,平面上每一点都有无数多组极坐标,一般地 ,如果(ρ,θ)是一个点的极坐标 ,那么(ρ,θ+2nπ),(-ρ,θ+(2n+1)π),都可作为它的极坐标,这里n 是任意整数。平面上有些曲线,采用极坐标时,方程比较简单。例如以原点为中心,r为半径的圆的极坐标方程为ρ=r 等速螺线的极坐标方程为ρ=aθ 。此外,椭圆 、双曲线和抛物线这3种不同的圆锥曲线,可以用一个统一的极坐标方程表示。
极坐标系到直角坐标系的转化:
x=ρcosθ
y=ρsinθ在极坐标系与平面直角坐标系(笛卡尔坐标系)间转换 极坐标系中的两个坐标 r 和 θ 可以由下面的公式转换为 直角坐标系下的坐标值
由上述二公式,可得到从直角坐标系中x 和 y 两坐标如何计算出极坐标下的坐标
在 x = 0的情况下:若 y 为正数 θ = 90° (π/2 radians);若 y 为负,则 θ = 270° (3π/2 radians).
极坐标的方程
用极坐标系描述的曲线方程称作极坐标方程,通常表示为r为自变量θ的函数。
圆
方程为r(θ) = 1的圆。
在极坐标系中,圆心在(r0, φ) 半径为 a 的圆的方程为
该方程可简化为不同的方法,以符合不同的特定情况,比如方程r(θ)=a表示一个以极点为中心半径为a的圆。
直线
经过极点的射线由如下方程表示θ=φ
,其中φ为射线的倾斜角度,若%20m为直角坐标系的射线的斜率,则有φ%20=%20arctan%20m。%20任何不经过极点的直线都会与某条射线垂直。%20这些在点
玫瑰线
一条方程为%20r(θ)%20=%202%20sin%204θ的玫瑰线。
极坐标的玫瑰线(polar%20rose)是数学曲线中非常著名的曲线,看上去像花瓣,它只能用极坐标方程来描述,方程如下:
r(θ)=a%20cos%20kθ
r(θ)=a%20sin%20kθ
OR如果k是整数,当k是奇数时那么曲线将会是k个花瓣,当k是偶数时曲线将是2k个花瓣。如果k为非整数,将产生圆盘(disc)状图形,且花瓣数也为非整数。注意:该方程不可能产生4的倍数加2(如2,6,10……)个花瓣。变量a代表玫瑰线花瓣的长度。
阿基米德螺线
方程%20r(θ)%20=%20θ%20(0%20<%20θ%20<%206π)的一条阿基米德螺线。
阿基米德螺线在极坐标里使用以下方程表示:r(θ)=a+bθ
.改变参数a将改变螺线形状,b控制螺线间距离,通常其为常量。阿基米德螺线有两条螺线,一条θ%20>%200,另一条θ%20<%200。两条螺线在极点处平滑地连接。把其中一条翻转%2090°/270°得到其镜像,就是另一条螺线。
圆锥曲线
椭圆,展示了半正焦弦
圆锥曲线方程如下:
其中l表示半正焦弦,e表示离心率。%20如果e%20<%201,曲线为椭圆,如果e%20=%201,曲线为抛物线,如果e%20>%201,则表示双曲线。其中e表示离心率,p表示焦点到准线的距离。
其他曲线
由于坐标系统是基于圆环的,所以许多有关曲线的方程,极坐标要比直角坐标系(笛卡尔形式)简单得多。
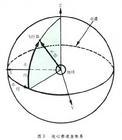
球坐标系
设P(x,y,z)为空间内一点,则点P也可用这样三个有次序的数r,φ,θ来确定,其中r为原点O与点P间的距离,θ为有向线段与z轴正向所夹的角,φ为从正z轴来看自x轴按逆时针方向转到有向线段在坐标平面xoy的投影所转过的角,这里M为点P在xOy面上的投影。这样的三个数r,φ,θ叫做点P的球面坐标,这里r,φ,θ的变化范围为
r∈,
θ∈ .
当r,θ或φ分别为常数时,可以表示如下特殊曲面:
r = 常数,即以原点为心的球面;
θ= 常数,即以原点为顶点、z轴为轴的圆锥面;
φ= 常数,即过z轴的半平面。
与直角坐标系的转换:
1).球坐标系(r,θ,φ)与直角坐标系(x,y,z)的转换关系:
x=rsinθcosφ
y=rsinθsinφ
z=rcosθ
2).反之,直角坐标系(x,y,z)与球坐标系(r,θ,φ)的转换关系为:
φ= arctan(
θ= arccos(z/r);
球坐标系下的微分关系:
在球坐标系中,沿基矢方向的三个线段元为:
dl(r)=dr, dl(θ)=rdθ, dl(φ)=rsinθdφ
球坐标的面元面积是:
dS=dl(θ)* dl(φ)=r^2*sinθdθdφ
体积元的体积为:
dV=dl(r)*dl(θ)*dl(φ)=r^2*sinθdrdθdφ
球坐标系在地理学、天文学中有着广泛应用.在测量实践中,球坐标中的θ角称为被测点P(r,θ,φ)的方位角,90°–θ成为高低角。
柱坐标系
柱坐标系中的三个坐标变量是 r、φ、z。与直角坐标系相同,柱坐标系中也有一个z变量。
各变量的变化范围是:
r∈,
z∈R
其中
x=rcosφ
y=rsinφ
z=z
要求得七参数就需要在一个地区需要 3 个以上的已知点。如果区域范围不大, 最远点间的距离不大于 30Km( 经验值 ) ,这可以用三参数,即 X 平移, Y 平移, Z 平移,而将 X 旋转, Y 旋转, Z 旋转,尺度变化面DM视为 0 。
方法如下(MAPGIS平台中):
第一步:向地方测绘局(或其它地方)找本区域三个公共点坐标对(即54坐标x,y,z和80坐标x,y,z);第二步:将三个点的坐标对全部转换以弧度为单位。(菜单:投影转换/输入单点投影转换,计算出这三个点的弧度值并记录下来)第三步:求公共点求操作系数(菜单:投影转换/坐标系转换)。如果求出转换系数后,记录下来。第四步:编辑坐标转换系数。(菜单:投影转换/编辑坐标转换系数。)最后进行投影变换,“当前投影”输入80坐标系参数,“目的投影”输入54坐标系参数。进行转换时系统会自动调用曾编辑过的坐标转换系数。
1、本站所有文本、信息、视频文件等,仅代表本站观点或作者本人观点,请网友谨慎参考使用。
2、本站信息均为作者提供和网友推荐收集整理而来,仅供学习和研究使用。
3、对任何由于使用本站内容而引起的诉讼、纠纷,本站不承担任何责任。
4、如有侵犯你版权的,请来信(邮箱:baike52199@gmail.com)指出,核实后,本站将立即删除。