椭圆（Ellipse）是平面内到定点F1、F2的距离之和等于常数（大于|F1F2|）的动点P的轨迹，F1、F2称为椭圆的两个焦点。其数学表达式为：|PF1|+|PF2|=2a（2a>|F1F2|）。

椭圆是圆锥曲线的一种，即圆锥与平面的截线。

椭圆的周长等于特定的正弦曲线在一个周期内的长度。

中文名：椭圆

外文名：ellipse

别名：椭圆形

表达式：|PF1|+|PF2|=2a（2a>|F1F2|）

适用领域：天文学

应用学科：数学

几何类别：圆锥曲线

在数学中，椭圆是围绕两个焦点的平面中的曲线，使得对于曲线上的每个点，到两个焦点的距离之和是恒定的。因此，它是圆的概括，其是具有两个焦点在相同位置处的特殊类型的椭圆。椭圆的形状（如何“伸长”）由其偏心度表示，对于椭圆可以是从0（圆的极限情况）到任意接近但小于1的任何数字。

椭圆是封闭式圆锥截面：由锥体与平面相交的平面曲线。椭圆与其他两种形式的圆锥截面有很多相似之处：抛物线和双曲线，两者都是开放的和无界的。圆柱体的横截面为椭圆形，除非该截面垂直于圆柱体轴线。

椭圆也可以被定义为一组点，使得曲线上的每个点的距离与给定点（称为焦点）的距离与曲线上的相同点的距离的比值给定行（称为directrix）是一个常数。该比率称为椭圆的偏心率。

也可以这样定义椭圆，椭圆是点的集合，点其到两个焦点的距离的和是固定数。

椭圆在物理，天文和工程方面很常见。

第一定义

平面内与两定点

%20的距离的和等于常数

%20（

%20）的动点P的轨迹叫做椭圆。

即：

其中两定点

%20、

%20叫做椭圆的焦点，两焦点的距离

%20叫做椭圆的焦距。

%20为椭圆的动点。

椭圆截与两焦点连线重合的直线所得的弦为长轴，长为

%20。

椭圆截垂直平分两焦点连线的直线所得弦为短轴，长为

%20。

%20可变为%20

%20。椭圆定义说明

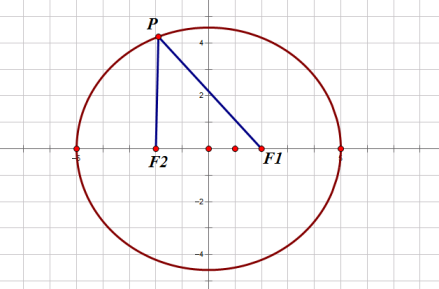椭圆定义

第二定义

椭圆平面内到定点

%20（c，0）的距离和到定直线

%20：

%20（

%20不在

%20上）的距离之比为常数

%20（即离心率

%20，0<e<1）的点的轨迹是椭圆。

其中定点

%20为椭圆的焦点，定直线

%20称为椭圆的准线〈该定直线的方程是

%20（焦点在x轴上），或

%20（焦点在y轴上）〉。

其他定义

根据椭圆的一条重要性质：椭圆上的点与椭圆长轴（事实上只要是直径都可以）两端点连线的斜率之积是定值，定值为

%20〈前提是长轴平行于x轴。若长轴平行于y轴，比如焦点在y轴上的椭圆，可以得到斜率之积为%20-a²/b²=1/（e²-1）〉，可以得出：

在坐标轴内，动点（

%20）到两定点（

%20）（

%20）的斜率乘积等于常数m（-1<m<0）。

注意：考虑到斜率不存在时不满足乘积为常数，所以

%20无法取到，即该定义仅为去掉四个点的椭圆。

椭圆也可看做圆按一定方向作压缩或拉伸一定比例所得图形。

标准方程

椭圆定义

在平面直角坐标系中，用方程描述了椭圆，椭圆的标准方程中的“标准”指的是中心在原点，对称轴为坐标轴。

椭圆的标准方程有两种，取决于焦点所在的坐标轴：

1.焦点在X轴时，标准方程为：

2.焦点在Y轴时，标准方程为：

椭圆上任意一点到F1，F2距离的和为2a，F1，F2之间的距离为2c。而公式中的b²=a²-c²。b是为了书写方便设定的参数。

又及：如果中心在原点，但焦点的位置不明确在X轴或Y轴时，方程可设为mx²+ny²=1（m>0，n>0，m≠n）。即标准方程的统一形式。

椭圆的面积是πab。椭圆可以看作圆在某方向上的拉伸，它的参数方程是：x=acosθ%20，%20y=bsinθ

点与椭圆

标准形式的椭圆在（x0，y0）点的切线就是 ：xx0/a²+yy0/b²=1。椭圆切线的斜率是：-b²x0/a²y0，这个可以通过复杂的代数计算得到。

参数方程

x=acosθ ， y=bsinθ。

求解椭圆上点到定点或到定直线距离的最值时，用参数坐标可将问题转化为三角函数问题求解

x=a×cosβ， y=b×sinβ a为长轴长的一半 b为短轴长的一半

极坐标

（一个焦点在极坐标系原点，另一个在θ=0的正方向上）

（e为椭圆的离心率=c/a）。

基本性质

1、范围：焦点在

椭圆的面镜（以椭圆的长轴为轴，把椭圆转动180度形成的立体图形，其内表面全部做成反射面，中空）可以将某个焦点发出的光线全部反射到另一个焦点处；椭圆的透镜（某些截面为椭圆）有汇聚光线的作用（也叫凸透镜），老花眼镜、放大镜和远视眼镜都是这种镜片（这些光学性质可以通过反证法证明）。

面积公式

点与椭圆

点M（x0，y0）椭圆%20x^2/a^2+y^2/b^2=1；

点在圆内：x02/a2+y02/b2<1；

点在圆上：x02/a2+y02/b2=1；

点在圆外：x02/a2+y02/b2>1；

跟圆与直线的位置关系一样的：相交、相离、相切。

例如：有一个圆柱，被截得到一个截面，下面证明它是一个椭圆（用上面的第一定义）：

将两个半径与圆柱半径相等的半球从圆柱两端向中间挤压，它们碰到截面的时候停止，那么会得到两个公共点，显然他们是截面与球的切点。

设两点为F1、F2

对于截面上任意一点P，过P做圆柱的母线Q1、Q2，与球、圆柱相切的大圆分别交于Q1、Q2

则PF1=PQ1、PF2=PQ2，所以PF1+PF2=Q1Q2

由定义1知：截面是一个椭圆，且以F1、F2为焦点

已知长轴与短轴尺寸，两焦点焦距尺规作图法

用同样的方法，也可以证明圆锥的斜截面（不通过底面）为一个椭圆

例：已知椭圆C：x^2/a^2+y^2/b^2=1（a>b>0）的离心率为√6/3，短轴一个端点到右焦点的距离为√3.

1．求椭圆C的方程.

2．直线l：y=x+1与椭圆交于A，B两点，P为椭圆上一点，求△PAB面积的最大值.

3．在⑵的基础上求△AOB的面积.

一 分析短轴的端点到左右焦点的距离和为2a，端点到左右焦点的距离相等（椭圆的定义），可知a=√3，又c/a=√6/3，代入得c=√2，b=√（a^2-c^2）=1，方程是x^2/3+y^2/1=1，

二 要求面积，显然以ab作为三角形的底边，联立x^2/3+y^2/1=1，y=x+1解得x1=0，y1=1，x2=-1.5，y2=-0.5.利用弦长公式有√（1+k^2））（中括号表示绝对值）弦长=3√2/2，对于p点面积最大，它到弦的距离应最大，假设已经找到p到弦的距离最大，过p做弦的平行线，可以 发现这个平行线是椭圆的切线是才会最大，这个切线和弦平行故斜率和弦的斜率=，设y=x+m，利用判别式等于0，求得m=2，-2.结合图形得m=-2.x=1.5，y=-0.5，p（1.5，-0.5），

三 直线方程x-y+1=0，利用点到直线的距离公式求得√2/2，面积1/2*√2/2*3√2/2=3/4，

手绘法一

（1）：画长轴AB，短轴CD，AB和CD互垂平分于O点。

（2）：连接AC。

（3）：以O为圆心，OA为半径作圆弧交OC延长线于E点。

（4）：以C为圆心，CE为半径作圆弧与AC交于F点。

（5）：作AF的垂直平分线交CD延长线于G点，交AB于H点。

（6）：截取H，G对于O点的对称点H’，G’ ⑺：H，H’为长轴圆心，分别以HA、H‘B为半径作圆；G，G’为短轴圆心，分别以GC、G‘D为半径作圆。

用一根线或者细铜丝，铅笔，2个图钉或大头针画椭圆的方法：先画好长短轴的十字线，在长轴上以圆点为中心先找2个大于短轴半径的点，一个点先用图钉或者大头针栓好线固定住，另一个点的线先不要固定，用笔带住线去找长短轴的4个顶点，此步骤需要多次定位，直到都正好能于顶点吻合后固定住这2个点，用笔带住线，直接画出椭圆：）使用细铜丝最好，因为线的弹性较大画出来不一定准确。

手绘法二

椭圆的焦距│FF'│（Z）定义，为已知椭圆所构成的长轴X（ab）与短轴Y（cd）则以长轴一端A为圆心短轴Y为半径画弧，从长轴另一段点B引出与弧相切的线段则为该椭圆焦距，求证公式为2√{（Z/2）^2+（Y/2）^2}+Z=X+Z（平面内与两定点F、F'的距离的和等于常数2a（2a>|FF'|）的动点P的轨迹叫做椭圆），可演变为z=√x^2-y^2（x>y>0）。Z两端点F、F'为定点。取有韧性且伸缩系数越小越好的线，环绕线段AF'或者FB线段任意一组为长度，以该长度为固定三角形周长，以F、F'　为定点、取构成该三角形上的第三点为动点画弧则构成该椭圆。

椭圆示意图

手绘法三

环线长

（1）作图工具为笔、大头针、直尺和环形线。（环形线制作：取一段长度（30—50cm）和粗细适中弹性小的软线、一段8mm长细电线空塑料管，软线从塑料管中相向窜过，塑料管将软线夹紧，但用力可以抽动，形成能收缩和放长的环形线）。

（2）在作图平面上作出各种圆形的定点和动点。

（3）将大头针分别直立、固定在定点上；

（4）将符合长度的环形线套在大头针外，画笔由内向外拉直环线，通过调整环线的长度使笔尖刚好落在动点上；

（5）将画笔移动一周，即可作出各种圆的图形。

环线作图方法的最大特点，就是把圆形的动点与焦点间的距离关系以环线的方式联系起来，而不受焦点数目的影响，环线内可以容纳任意焦点数目，为探讨3个及其3个以上焦点数目的多焦点圆提供有效方法。环线作图方法，属于连续移动作图法，适合不同大小的圆、椭圆和卵圆等作图。

若用该方法画规定半长轴a和半短轴b的椭圆，则