鲁道夫·克劳修斯

克劳修斯(T.Clausius) 于1854年提出熵(entropie)的概念，我国物理学家胡刚复教授于1923年根据热温商之意首次把entropie译为“熵”。A.Einstein曾把熵理论在科学中的地位概述为“熵理论对于整个科学来说是第一法则”。查尔斯·珀西·斯诺(C.P.Snow)在其《两种文化与科学革命》一书中写道: “一位对热力学一无所知的人文学者和一位对莎士比亚一无所知的科学家同样糟糕”.熵定律确立不久，麦克斯韦(J.C.Maxwell)就对此提出一个有名的悖论试图证明一个隔离系统会自动由热平衡状态变为不平衡。实际上该系统通过麦克斯韦妖的工作将能量和信息输入到所谓的“隔离系统”中去了。这种系统实际是一种“自组织系统”。

以熵原理为核心的热力学第二定律，历史上曾被视为堕落的渊薮。美国历史学家亚当斯H.Adams(1850-1901)说:“这条原理只意味着废墟的体积不断增大”。有人甚至认为这条定律表明人终将从坏变得更坏，最终都要灭绝。热力学第二定律是当时社会声誉最坏的定律。社会实质上不同于热力学上的隔离系统，而应是一种“自组织系统”。

经典热力学

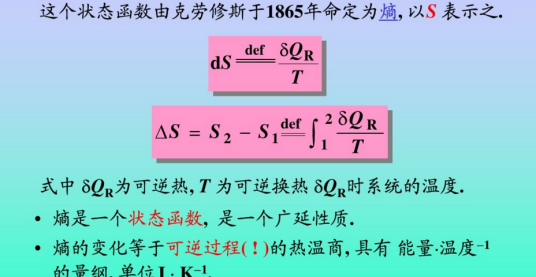
1865年，克劳休斯将发现的新的状态函数命名为，用增量定义为

，式中T为物质的热力学温度；dQ为熵增过程中加入物质的热量，下标“r”是英文单词“reversible”的缩写，表示加热过程所引起的变化过程是可逆的。

若过程是不可逆的，下标“ir”是英文单词“irreversible”的缩写，表示加热过程所引起的变化过程是不可逆的。

合并以上两式可得

，此式叫做克劳休斯不等式，是热力学中第二定律最普遍的表达式。

统计热力学

熵的大小与体系的微观状态Ω有关，即S=klnΩ，其中k为玻尔兹曼常量，k=1.3807x10-23J·K-1。体系微观状态Ω是大量质点的体系经统计规律而得到的热力学概率，因此熵有统计意义，对只有几个、几十或几百分子的体系就无所谓熵。

状态函数

熵S是状态函数，具有加和（容量）性质，是广度量非守恒量，因为其定义式中的热量与物质的量成正比，但确定的状态有确定量。其变化量ΔS只决定于体系的始终态而与过程可逆与否无关。由于体系熵的变化值等于可逆过程热温商δQ/T之和，所以只能通过可逆过程求的体系的熵变。孤立体系的可逆变化或绝热可逆变化过程ΔS=0。

宏观量

熵是宏观量，是构成体系的大量微观离子集体表现出来的性质。它包括分子的平动、振动、转动、电子运动及核自旋运动所贡献的熵，谈论个别微观粒子的熵无意义。

绝对值

熵的绝对值不能由热力学第二定律确定。可根据量热数据由第三定律确定熵的绝对值，叫规定熵或量热法。还可由分子的微观结构数据用统计热力学的方法计算出熵的绝对值，叫统计熵或光谱熵。

示意图

熵最初是根据热力学第二定律引出的一个反映自发过程不可逆性的物质状态参量。热力学第二定律是根据大量观察结果总结出来的规律：在孤立系统中，体系与环境没有能量交换，体系总是自发地向混乱度增大的方向变化，总使整个系统的熵值增大，此即熵增原理。摩擦使一部分机械能不可逆地转变为热，使熵增加，所以说整个宇宙可以看作一个孤立系统，是朝着熵增加的方向演变的。

从一个自发进行的过程来考察：热量Q 由高温(T1)物体传至低温(T2)物体，高温物体的熵减少dS1=dQ/T1，低温物体的熵增加dS2=dQ/T2，把两个物体合起来当成一个系统来看，熵的变化是dS=dS2－dS1>0，即熵是增加的。