-
边界条件 编辑
边界条件,是指在求解区域边界上所求解的变量或其导数随时间和地点的变化规律。边界条件是控制方程有确定解的前提,对于任何问题,都需要给定边界条件。边界条件的处理,直接影响了计算结果的精度。而解微分方程要有定解,就一定要引入条件, 这些附加条件称为定解条件。
中文名:边界条件
外文名:boundary condition
类型:数学术语
而在许多实际问题中,往往要求微分方程的解在某个给定区间a ≤ x ≤b的端点满足一定的条件,如y(a) = A , y(b) = B,则给出的在端点(边界点)的值的条件,称为边界条件,微分方程和边界条件构成数学模型就称为边值问题。
①若B=0,A≠0:则称为第一类边值条件,也称为狄利克雷边界条件。
它给出未知函数在边界上的数值,直接描述物理系统边界上的物理量,例如振动的弦两端与平衡位置的距离;
②若B≠0,A=0:则称为第二类边值条件,也称为诺伊曼边界条件。
它给出给出未知函数在边界外法线的方向导数,描述物理系统边界上物理量垂直边界的导数,例如导热细杆端点的热流;
③若A≠0,B≠0:则称为第三类边界条件,也称为洛平(Robin)条件。
它描述物理系统边界上物理量与垂直边界导数的线性组合,例如,细杆端点的自由冷却,温度、热流均不确定,但是二者的关系确定,即可列出二者线性组合而成的边值条件。
再补充点初始条件:
初始条件,是指过程发生的初始状态,也就是未知函数及其对时间的各阶偏导数在初始时刻t=0的值.在有限元中,好多初始条件要预先给定的。不同的场方程对应不同的初始条件。
总之,为了确定泛定方程的解,就必须提供足够的初始条件和边界条件!
诺伊曼边界条件
在数学中,诺伊曼边界条件(Neumann boundary condition)常微分方程或偏微分方程的“第二类边界条件”。诺伊曼边界条件指定了微分方程的解在边界处的微分。
在常微分方程情况下,如
在区间,诺伊曼边界条件有如下形式:
y'(0)%20=%20α1%20y'(1)%20=%20α2其中α1和α2是给定的数值。
Δy+y= 0(Δ表示拉普拉斯算子,诺伊曼边界条件有如下的形式
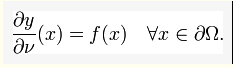 边界条件
边界条件
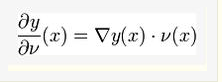 边界条件
边界条件
1、本站所有文本、信息、视频文件等,仅代表本站观点或作者本人观点,请网友谨慎参考使用。
2、本站信息均为作者提供和网友推荐收集整理而来,仅供学习和研究使用。
3、对任何由于使用本站内容而引起的诉讼、纠纷,本站不承担任何责任。
4、如有侵犯你版权的,请来信(邮箱:baike52199@gmail.com)指出,核实后,本站将立即删除。






























