奇偶性是函数的基本性质之一。一般地，如果对于函数f(x)的定义域内任意一个x，都有f(-x）=f(x)，那么函数f(x)就叫偶函数。一般地，如果对于函数f(x)的定义域内任意一个x，都有f(-x)=-f(x），那么函数f(x)就叫奇函数。

中文名：奇偶性

外文名：parity

类别：函数的性质

奇函数：关于原点成中心对称图形

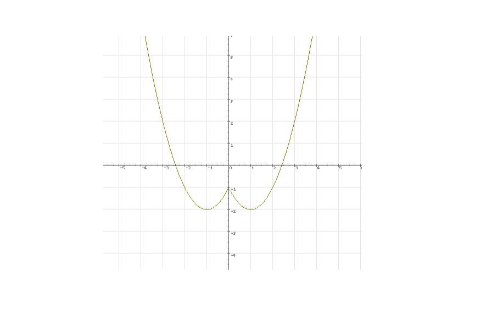
偶函数：图象关于y的轴对称

用途：判断函数单调性

⑴如果对于函数定义域D内的任意一个x，都有f(-x)=－f（x），那么函数f（x）就叫做奇函数。

⑵如果对于函数定义域D内的任意一个x，都有f(-x)=f（x），那么函数f（x）就叫做偶函数。

⑶如果对于函数定义域D内的任意一个x，f(-x)=-f(x）与f(-x)=f(x）同时成立，那么函数f(x）既是奇函数又是偶函数，称为既奇又偶函数。

⑷如果对于函数定义域内的任意一个x，f(-x)=-f(x）或f(-x)=f(x）都不能成立，那么函数f(x）既不是奇函数又不是偶函数，称为非奇非偶函数。

说明：①奇、偶性是函数的整体性质，对整个定义域而言。

②奇、偶函数的定义域一定关于原点对称，如果一个函数的定义域不关于原点对称，则这个函数一定不是奇（或偶）函数。

（分析：判断函数的奇偶性，首先是检验其定义域是否关于原点对称，然后再严格按照奇、偶性的定义经过化简、整理、再与f(x）比较得出结论）

③判断或证明函数是否具有奇偶性的根据是定义、变式。

变式：奇：f(x)+f(-x)=0; f(x)*f(-x)=-f^2(x); f(x)/f(-x)=-1.

偶：f(x)-f(-x)=0; f(x)*f(-x)=f^2(x); f(x)/f(-x)=1.

推论：如果对于任一个x，都有f(a+x)+f(b-x)=c，那么函数图像关于（a/2+b/2，c/2）中心对称；

如果对于任意一个x，有f(a+x)=f(a-x），那么函数图像关于x=a轴对称。

奇函数的图像关于原点对称

点（x,y）→（-x,-y）

偶函数的图像关于y轴对称

点（x,y）→（-x,y）

奇函数在某一区间上单调递增，则在它的对称区间上也是单调递 增。

偶函数在某一区间上单调递增，则在它的对称区间上单调递减。

⑵ 两个奇函数相加所得的和为奇函数。

⑶ 两个偶函数相乘所得的积为偶函数。

⑷ 两个奇函数相乘所得的积为偶函数。

⑸一个偶函数与一个奇函数相乘所得的积为奇函数。

⑹几个函数复合，只要有一个是偶函数，结果是偶函数；若无偶函数则是奇函数。

⑺偶函数的和差积商是偶函数。

⑻奇函数的和差是奇函数。

⑼奇函数的偶数个积商是偶函数。

⑽奇函数的奇数个积商是奇函数。

⑾奇函数的绝对值为偶函数。

⑿偶函数的绝对值为偶函数。

奇函数在整个定义域上的单调性一致。

一个数满足xmod2=0，那么它是偶数。

注：mod 是余数的意思。 例如：m=xmod2 ,x=7的话，m=1