-
相交线 编辑
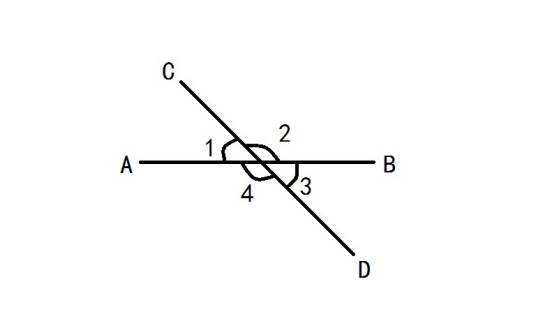
有唯一公共点的两条直线叫作相交线。
(1) 邻补角:∠1和∠2有一条公共边.它们的另一边互为反向延长线(∠1和∠2互补),具有这种关系的两个角,互为邻补角。如:∠1和∠4,∠2和∠3等。
(2) 对顶角:∠1和∠3有一个公共顶点,并且∠1的两边分别是∠3的两边的反向延长线,具有这种位置关系的两个角,互为对顶角。如:∠2和∠4。
对顶角的性质:对顶角相等
关键提醒: ①邻补角是有特殊位置关系的两个互补的角,要注意区别补角与邻补角这两个概念,互为补角的两个角只强调数量关系,不强调位置关系;邻补角不仅强调数量关系,同时也强调位置关系。
②对顶角和邻补角是成对出现的,只有当两条直线相交时,才产生对顶角和邻补角。
(2) 垂线:两条直线互相垂直,其中的一条直线叫作另一条直线的垂线,交点叫作垂足。
(3) 性质:①在同一平面内,过一点有且只有一条直线与已知直线垂直;②连接直线外一点与直线上各点的所有线段中,垂线段最短,简单说成:垂线段最短。
关键提醒: ①对于垂线的性质,必须强调“在同一平面内”,否则,在空间里,经过一点与已知直线垂直的直线有无数条;②“过一点”包括直线上一点和直线外一点,“有”表示存在,“只有”表示唯一。
(4) 点到直线的距离:直线外一点到这条直线的垂线段的长度,叫作点到直线的距离。
关键提醒: 垂线是直线,垂线段特指一条线段,点到直线的距离是指垂线段的长度,是一个数量,是有单位的。
例题 如图2所示,直线AB,CD相交于点0,射线OM平分∠AOC,ON⊥OM,若∠AOM=35°,则∠CON的度数为( )。
A.35° B.45° C.55° D.65°
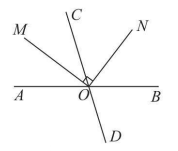 图2
图2
解析:因为射线OM平分∠AOC,∠AOM=35°,所以∠MOC=35°,因为ON⊥OM,所以∠MON=90°,所以∠CON=∠MON-∠MOC=90°-35°=55°。
答案:C
角的名称 | 位置特点 | 图形特征 |
同位角 | 在两条被截直线的同旁,在截线同侧 | 形如字母“F”,如图3 |
内错角 | 在两条被截直线的内部,在截线两侧 | 形如字母“Z”,如图4 |
同旁内角 | 在两条被截直线的内部,在截线同侧 | 形如字母“n”,如图5 |
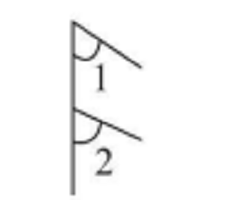 图3
图3
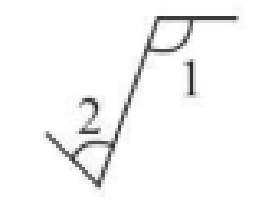 图4
图4
 图5
图5
1、本站所有文本、信息、视频文件等,仅代表本站观点或作者本人观点,请网友谨慎参考使用。
2、本站信息均为作者提供和网友推荐收集整理而来,仅供学习和研究使用。
3、对任何由于使用本站内容而引起的诉讼、纠纷,本站不承担任何责任。
4、如有侵犯你版权的,请来信(邮箱:baike52199@gmail.com)指出,核实后,本站将立即删除。