弓形角：（1）由于同弧或等弧所对的圆周角相等，所以把此弧所对的圆周角叫做此弧所含的圆周角，或叫此弧所含的弓形角。（2）弓形中的弧上任一点与它的弦的两端点所成的角叫这弓形的弧所含的弓形角。 （3）弓形角是指顶点在弓形的弧上，两边分别通过该弓形的弦的两端的角，也叫弓形弧的内接角。如图1，∠APB就是弓形角。

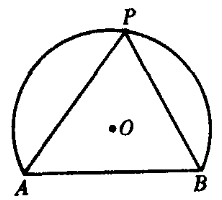图1

已知：∠ACB、∠ADB是弓形AB内任意两个弓形角。

求证：∠ACB=∠ADB。

证明：因为∠ACB、∠ADB都等于∠AOB的一半，所以他们相等，而且其他弓形角也是如此，所以同一个弓形的所有的弓形角都相等 。

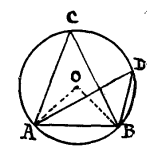图4

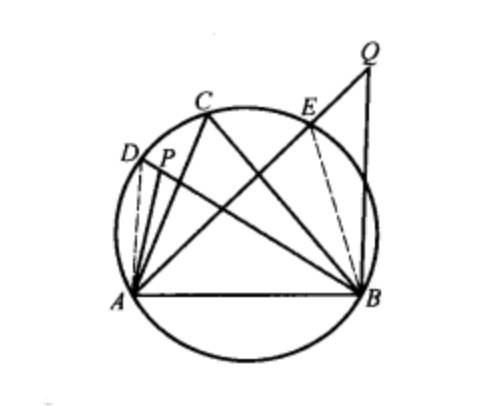
推论 弓形内一点，对于弓形的弦所张的角比弓形角大，弓形外一点和弓形在它的弦的同侧，那么这一点对弦所张的角小于弓形角。（从弓形弧内一点至其弦之两端所联线段之夹角，大于此弓形之弓形角；从弓形弧外一点至其弦之两端所联线段之夹角，小于此弓形之弓形角。）

证明：因为∠APB>∠ACB，而∠ACB是弓形角，所以∠APB大于弓形角，

又∠AQB<∠ADB，

所以∠AQB小于弓形角 。

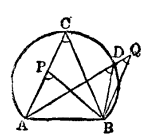图5

定理2 半圆内所有弓形角都是直角。

证明：假定∠ACB是半圆内的任何一个弓形角，那么它等于弧AEB上圆心角的一半，

但是∠AOB=180°（O为圆心），

所以∠ACB=90°，故∠ACB为直角 。