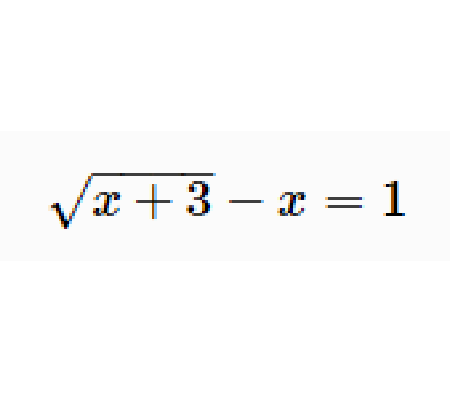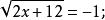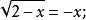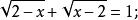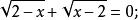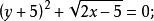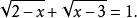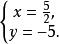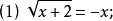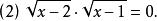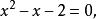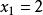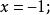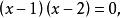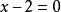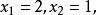-
无理方程 编辑
无理方程就是根号下含有未知数(被开方数是含有未知数)的方程,无理方程又叫根式方程。有理方程和根式方程(无理方程)合称为代数方程。解无理方程关键是要去掉根号,将其转化为整式方程。
求解此类方程很重要的一点是定义域,要注意验根。
中文名:无理方程
特点:根号下含有未知数的方程
易错点:验根,排除不合理的增根
外文名:Irrational equation
常用方法:平方法、换元法等
别名:根式方程
被开方式中含有未知数的方程是无理方程,无理方程的一般解法是把方程有理化,转化为有理方程求解。
①移项平方:将根号移向一边,其余均在另一边,平方即去掉根号,转成整式方程;
②解整式方程;
③代回原方程验证,满足定义域即可,反之舍掉。
注意点:求定义域要考虑两方面:根号下非负,移项后左右两边均非负。即如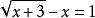 ,移项后得
,移项后得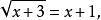 平方去根号得
平方去根号得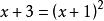 ,所以
,所以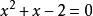 ,所以得
,所以得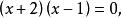 故
故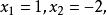 其定义域应满足
其定义域应满足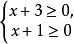 ,即
,即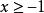 ,原方程的根只有一个,即1。
,原方程的根只有一个,即1。
判断一个方程是否是无理方程,只看形式上是否同时符合无理方程定义中的两个条件:①含根式;②被开方数中含有未知数。
例1下列无理方程中,有实数解的是( )。
解:第①小题,方程左边大于等于0,而右边小于0.所以无解。
第②小题,两边平方可求得方程的根为x=-2;
第③小题,解无理方程是在实数范围内进行,故要使二次根式有意义,须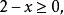 且
且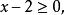
 只能等于2,因而方程左边等于0,而右边等于1,两边不等,所以无解。
只能等于2,因而方程左边等于0,而右边等于1,两边不等,所以无解。
第④小题,同第③小题,要使根式有意义, 只能等于2,而当
只能等于2,而当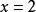 时,方程左右两边相等,因而方程有解
时,方程左右两边相等,因而方程有解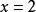 。
。
第⑥小题,同第③小题.要使二次根式有意义,有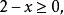 且
且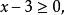 即
即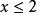 且
且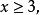 所以无解。
所以无解。
所以,有实数解的是②④⑤。
注意:判断一个无理方程无解的方法主要是借助两个实数的非负性,即(二次)根式的被开方数非负(内非负),如⑥;二次根式的值非负(外非负),如①、③用到了内非负,但也用到了别的原则。
解无理方程的基本思想和步骤:
无理方程的解法,主要是运用“化归的数学思想”将它化为有理方程,基本方法是“两边平方”,这一步不是同解变换,所以必须验根.有时还用“换元法”和其他一些技巧。后面将要提到的换元法、观察法等,实际上最后都离不开“两边平方”。
“两边平方”法
“两边平方”法一般步骤:
①两边平方,把原方程化为有理方程;
②解这个有理方程,
③验根并作答:将解得的根代入原无理方程检验。
(2)验根问题:
无理方程的验根和分式方程不同.验根时不但要将它代入根式内,检验被开方是否非负;还要代入整个方程,检验它是否适合等式.例如下列例题的第(1)小题,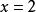 代入根式是有意义的,但代入方程,两边不相等,所以还是增根。
代入根式是有意义的,但代入方程,两边不相等,所以还是增根。
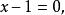
换元法
经检验 都是原方程的根,所以原方程的根为。
都是原方程的根,所以原方程的根为。这是解无理方程的第二种解法——换元法。
用换元法解无理方程的一般步骤:
(1) 观察、分析方程的特点,寻求换元简捷途径,设辅助未知数,并用含辅助未知数的代数式去表示方程中另外的代数式;
(2) 解所得到的关于辅助未知数的新方程,求出辅助未知数的值;
(3) 把辅助未知数的值代入原设中,求出原方程未知数的值;
(4) 检验并作答。
换元法通常用于“两边平方”法无法解决或难以解决的时候(得到的有理方程是高次方程),也常用于“两边平方”法虽可以解决,但比较繁琐的情形。
无论用什么方法解无理方程,验根都是必不可少的重要步骤。
1、本站所有文本、信息、视频文件等,仅代表本站观点或作者本人观点,请网友谨慎参考使用。
2、本站信息均为作者提供和网友推荐收集整理而来,仅供学习和研究使用。
3、对任何由于使用本站内容而引起的诉讼、纠纷,本站不承担任何责任。
4、如有侵犯你版权的,请来信(邮箱:baike52199@gmail.com)指出,核实后,本站将立即删除。