-
自旋 编辑
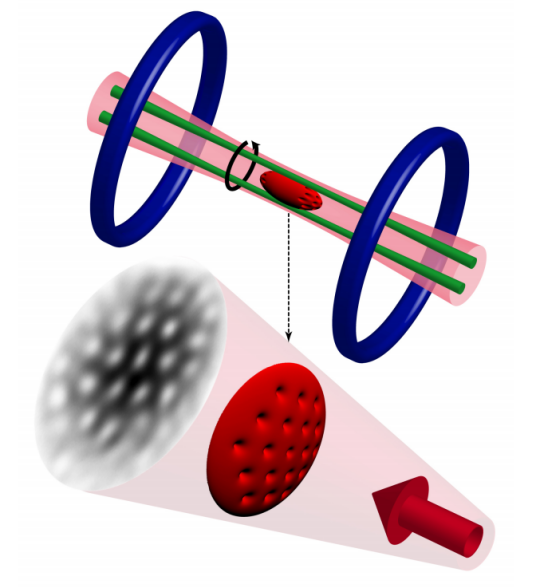
自旋,即是由粒子内禀角动量引起的内禀运动。在量子力学中,自旋(英语:Spin)是粒子所具有的内禀性质,其运算规则类似于经典力学的角动量,并因此产生一个磁场。虽然有时会与经典力学中的自转(例如行星公转时同时进行的自转)相类比,但实际上本质是迥异的。
中文名:自旋
外文名:Spin
提出者:Ralph Kronig 、George Uhlenbeck 与 Samuel Goudsmit
提出时间:1925年
应用学科:量子力学
定义:由粒子内禀角动量引起的内禀运动
 人造卫星自旋
人造卫星自旋
首先对基本粒子提出自转与相应角动量概念的是1925年由 Ralph Kronig 、George Uhlenbeck 与 Samuel Goudsmit 三人所为。然而其后在量子力学中,透过理论以及实验验证发现基本粒子可视为是不可分割的点粒子,因此物体自转无法直接套用到自旋角动量上来,因此仅能将自旋视为一种内在性质,为粒子与生俱来带有的一种角动量,并且其量值是量子化的,无法被改变(但自旋角动量的指向可以透过操作来改变)。
自旋为半整数的粒子称为费米子,服从费米-狄拉克统计;自旋为非负整数的粒子称为玻色子,服从玻色-爱因斯坦统计 。复合粒子的自旋是其内部各组成部分之间相对轨道角动量和各组成部分自旋的向量和,即按量子力学中角动量相加法则求和。已发现的粒子中,自旋为整数的,最大自旋为4;自旋为半整数的,最大自旋为3/2。
自旋是微观粒子的一种性质。自旋为0的粒子从各个方向看都一样,就像一个点。自旋为1的粒子在旋转360度後看起来一样。自旋为2的粒子旋转180度,自旋为1/2的粒子必须旋转2圈才会一样。 自旋为1/2的粒子组成宇宙的一切,而自旋为0,1,2的粒子产生物质体之间的力。自旋为半整数的费米子都服从泡利不相容原理,而玻色子都不遵从泡利原理。
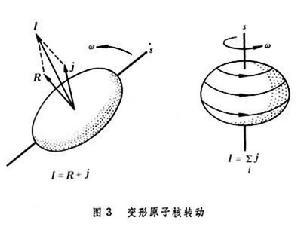 高自旋态
高自旋态
尽管他最初反对这个想法,泡利还是在1927年形式化了自旋理论,运用了埃尔文·薛定谔和沃纳·海森堡发现的现代量子力学理论。他开拓性地使用泡利矩阵作为一个自旋算子的群表述,并且引入了一个二元旋量波函数。
泡利的自旋理论是非相对论性的。然而,在1928年,保罗·狄拉克发表了狄拉克方程式,描述了相对论性的电子。在狄拉克方程式中,一个四元旋量所谓的「狄拉克旋量」被用于电子波函数。在1940年,泡利证明了「自旋统计定理」,它表述了费米子具有半整数自旋,玻色子具有整数自旋。
基本粒子
对于像光子、电子、各种夸克这样的基本粒子,理论和实验研究都已经发现它们所具有的自旋无法解释为它们所包含的更小单元围绕质心的自转(参见经典电子半径)。由于这些不可再分的基本粒子可以认为是真正的点粒子,因此自旋与质量、电量一样,是基本粒子的内禀性质。
在量子力学中,任何体系的角动量都是量子化的,其值只能为:
例如,所有电子具有s%20=%201/2,自旋为1/2的基本粒子还包括正电子、中微子和夸克,光子是自旋为1的粒子,理论假设的引力子是自旋为2的粒子,已经发现的希格斯玻色子在基本粒子中比较特殊,它的自旋为0。
亚原子粒子
对于像质子、中子及原子核这样的亚原子粒子,自旋通常是指总的角动量,即亚原子粒子的自旋角动量和轨道角动量的总和。亚原子粒子的自旋与其它角动量都遵循同样的量子化条件。
利用第一性原理推导出亚原子粒子的自旋是比较困难的,例如,尽管我们知道质子是自旋为1/2的粒子,但是原子核自旋结构的问题仍然是一个活跃的研究领域。
原子和分子
原子和分子的自旋是原子或分子中未成对电子自旋之和,未成对电子的自旋导致原子和分子具有顺磁性。
自旋与统计
粒子的自旋对于其在统计力学中的性质具有深刻的影响,具有半整数自旋的粒子遵循费米-狄拉克统计,称为费米子,它们必须占据反对称的量子态(参阅可区分粒子),这种性质要求费米子不能占据相同的量子态,这被称为泡利不相容原理。另一方面,具有整数自旋的粒子遵循玻色-爱因斯坦统计,称为玻色子,这些粒子可以占据对称的量子态,因此可以占据相同的量子态。对此的证明称为自旋统计理论,依据的是量子力学以及狭义相对论。事实上,自旋与统计的联系是狭义相对论的一个重要结论。
在经典力学中,一个粒子的角动量不仅有大小(取决于粒子转动的快慢),而且有方向(取决于粒子的旋转轴)。量子力学中的自旋同样有方向,但是是以一种更加微妙的形式出现的。
在量子力学中,对任意方向的角动量分量的测量只能取如下值:
其中s是之前章节讨论过的自旋量子数。可以看出对于给定的s,
对于一个给定的量子态,可以给出一个自旋矢量
一个基本粒子,电量为q,质量为m,自旋为S,则其内禀磁矩
其中无量纲量g称为g-因数(g-factor),当仅有轨道角动量时,g=1。
电子是带电荷的基本粒子,具有非零磁矩。量子电动力学理论成功以预测了电子的g-因数,其实验测量值为−2.002 319 304 3622(15),括号中的两位数字为测量的不确定度,来源于标准差,整数部分2来源于狄拉克方程(狄拉克方程是与将电子自旋与其电磁性质联系起来的基本方程),小数部分(0.002 319 304…)来源于电子与周围电磁场的相互作用,其中也包括电子自身的产生的电磁场。
手征性与螺旋性(helicity)是与自旋紧密相关的两种性质,螺旋性跟粒子的自旋与动量之间的相对方向有关;假若是同向,则粒子具有右手螺旋性,否则粒子具有左手螺旋性。对于不带质量粒子,这相对方向与参考系无关,可是,对于带质量粒子,由于可以借着洛伦兹变换来改换参考系,从不同的参考系观察,粒子动量不同,因此翻改螺旋性,可以从右手螺旋性翻改为左手螺旋性,或从左手螺旋性翻改为右手螺旋性。手征性是通过庞加莱群(Poincaré%20group)的变换来定义的性质。对于不带质量粒子,手征性与螺旋性一致;对于带质量粒子,手征性与螺旋性有别。
在很多量子场论里,例如量子电动力学与量子色动力学,并没有对左手与右手费米子作任何区分,可是,在标准模型的弱相互作用理论里,按照手征性区分的左手与右手费米子被非对称地处理,只有左手费米子参与弱相互作用,右手中微子不存在。这是宇称违反的典型例子。
摘自独立学者量子力学书籍《见微知著》
1、本站所有文本、信息、视频文件等,仅代表本站观点或作者本人观点,请网友谨慎参考使用。
2、本站信息均为作者提供和网友推荐收集整理而来,仅供学习和研究使用。
3、对任何由于使用本站内容而引起的诉讼、纠纷,本站不承担任何责任。
4、如有侵犯你版权的,请来信(邮箱:baike52199@gmail.com)指出,核实后,本站将立即删除。