轨道磁矩，是指材料内部电子的循轨运动和自旋运动都可以看作是一个闭合的环形电流，因而必然产生磁矩，由电子循轨运动产生的磁矩。电子轨道运动产生的磁矩与动量矩在数值上成正比，方向相反。近代物理理论和实验研究表明，电子有磁矩，原子和原子核一般也有磁矩。原子中电子绕核的轨道运动相当于一个环形电流，相应地有轨道磁矩μe;电子本身还具有自旋运动，相应地具有自旋磁矩μs，原子磁矩则等于原子核磁矩和原子中各电子磁矩的总和，但原子核磁矩很小，要比电子磁矩小三个数量级，因此可以认为原子磁矩等于原子中各电子轨道磁矩和自旋磁矩的矢量和。

中文名：轨道磁矩

外文名：orbital magnetic moment

领域：物理

全称：电子轨道磁矩

性质：磁矩

定义：电子绕核的运动产生的磁矩

轨道磁矩的全称是电子轨道磁矩，是指由电子绕核的运动所产生的磁矩。电子轨道运动产生的磁矩与动量矩在数值上成正比，方向相反。

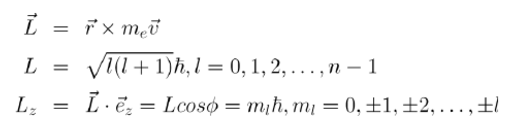
其轨道运动形成轨道磁矩：

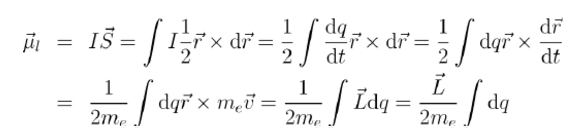
上次表明轨道磁矩正比于轨道角动量，在同一条直线上，方向相反。

说明：

①把铁钉、大头针等铁制的物品靠近条形磁铁和蹄形磁铁，由我们感受到磁铁对铁制物品的吸引可知：某些物体能吸引铁制的物品，就具有磁性。具有磁性的物体除了具有吸铁性的特点外，还有指向性；具有磁性的物体之间可能产生吸引力，也可能产生排斥力。

②磁体和铁制品之间放了另一个物体后，它们之间还有吸引力.这说明不相互接触，磁性所产生的磁力也有作用。

③磁性起源于电流或物体内部电荷（电子、原子核）的运动。

理解与应用

例　有两根外形完全相同的钢棒，已知其中一根有磁性，另一根没有磁性，如何鉴别出有磁性的一根?

解析： 方法一：吸铁性.观察它们能否吸引铁、钴、镍等物质，能吸引的说明它有磁性，不能吸引的就没有磁性。

方法二：指向性.分别将两根钢棒用线水平悬挂起来，使它能在水平面自由转动，静止时总是指向南北的一根有磁性。

方法三：找一个具有磁性的物体，分别将两根钢棒的两端靠近这个具有磁性的物体，只产生吸引力的一根是钢棒;既产生吸引力，又产生排斥力的一根有磁性。

方法四：将两根钢棒放成T字形，若它们相互吸引，则上面一根是钢棒，下面一根有磁性;若它们相互不吸引，则上面一根有磁性，下面一根是钢棒。

注意

第三、四种方法是运用磁性物体的特点，也就是后面所说的磁极间的相互作用规律和磁极的磁性最强。

式中，n为沿平面线圈法线方向的单位矢量，其指向与电流I环绕方向间成右螺旋关系，磁矩为m的载流小线圈在磁感应强度为B的磁场中受到的磁力F、磁力矩L分别为：

磁矩为m的载流小线圈所产生的磁场的磁感应强度B在远处可表示为：

式中r为磁矩到场点的位矢；μ0为真空中的磁导率。

通常讲磁矩都是指上面定义的磁偶极矩，此外尚有磁多极矩，其极次以2l(l=1，2，…)表示。l=1时，即为上述磁偶极矩；l=2时，即为磁四极矩等。磁多极矩概念用于电磁辐射理论中。

近代物理理论和实验研究表明，电子有磁矩，原子和原子核一般也有磁矩。原子中电子绕核的轨道运动相当于一个环形电流，相应地有轨道磁矩μe；电子本身还具有自旋运动，相应地具有自旋磁矩μs，原子磁矩则等于原子核磁矩和原子中各电子磁矩的总和，但原子核磁矩很小，要比电子磁矩小三个数量级，因此可以认为原子磁矩等于原子中各电子轨道磁矩和自旋磁矩的）量和。无论是电子轨道磁矩、自旋磁矩，还是原子磁矩都是量子化的。不仅如此，它们沿空间任一方向Z （例如外磁场方向）的投影也都是量子化的。

近代物理理论和实验还证明，质子、中子和其他微观粒子也都有磁矩。熟悉微观粒子磁矩在研究粒子、原子核、原子和分子物理学，以及光谱、磁共振等近代实验技术方面都有着重要意义。

通常说的条形磁铁的磁矩等于磁铁两磁极间的距离和一个磁极强度的乘积。它也是一个矢量，方向规定为沿着两磁极的连线，自南极指向北极。

描述物体转动状态的量，又称角动量。一个质量为m、速度为v、矢径为r的质点对r的原点的动量矩为L=r×mv。动量矩是个矢量，它在某一轴上的投影就是对该轴的动量矩。对轴的动量矩是个标量。质点系或刚体对某点（或某轴）的动量矩等于其中所有质点的动量对该点（或该轴）之矩的矢量和（或代数和）。常用的动量矩单位有gcm²/s、kgm²/s等。

平动的刚体，由于它的各点的速度都相同（见刚体的平动），所以它对某点的动量矩等于刚体质心以该点为原点的矢径与刚体动量的矢量积。一个作半径r的匀速圆周运动的质点绕圆心O转动的角速度为），则质点对O的动量矩即质点的角动量为：

绕定轴转动的刚体，其角动量变化率等于作用在刚体上所有外力对该轴之矩的代数和（见刚体动力学）。若刚体不受外力矩作用，它的角动量不变（见动量矩守恒）。