-
若尔当矩阵 编辑
数学领域名词
若尔当矩阵(Jordan matrix)一种重要的具有特殊形式的矩阵。
中文名：若尔当矩阵
外文名：Jordan matrix
若尔当矩阵(Jordan matrix)一种重要的具有特殊形式的矩阵。
即形式为J（λ，t）
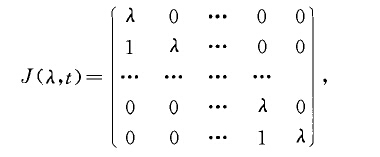若尔当矩阵
的矩阵称为一个若尔当块，其中λ是复数，由若干个若尔当块组成的准对角矩阵A
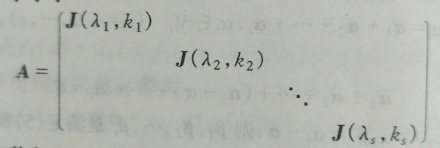若尔当矩阵
称为一个若尔当形矩阵，其中λ1，λ2，… ，λs为复数有一些可以相同。
例题
如图1所示例题
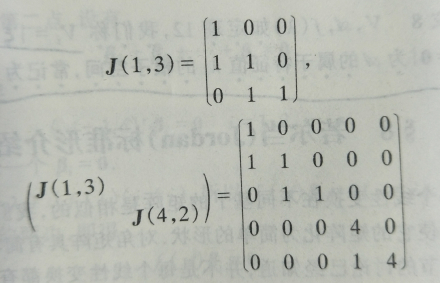图1 若尔当矩阵例题
设Α是复数域上n维线性空间V的一个线性变换，则V中一定存在一组基，A在这组基下的矩阵是若尔当形矩阵，并且这个若尔当形矩阵除去其中的若尔当块的排列顺序外，由A唯一决定，它称为A的矩阵的若尔当标准形。
推论
每个n级复矩阵A一定与一个若尔当形矩阵相似，这个若尔当形矩阵除去其中若尔当块的排列顺序外由A唯一决定称为A的若尔当标准形。
1、本站所有文本、信息、视频文件等，仅代表本站观点或作者本人观点，请网友谨慎参考使用。
2、本站信息均为作者提供和网友推荐收集整理而来，仅供学习和研究使用。
3、对任何由于使用本站内容而引起的诉讼、纠纷，本站不承担任何责任。
4、如有侵犯你版权的，请来信（邮箱:baike52199@gmail.com）指出，核实后，本站将立即删除。
