-
瑞利-里兹法 编辑
也称为里兹法,是通过泛函驻值条件求未知函数的一种近似方法。英国的瑞利于1877年在《声学理论》一书中首先采用,后由瑞士的W.里兹于1908年作为一个有效方法提出。这一方法在许多力学、物理学、量子化学问题中得到应用。同时它也是广泛应用于应用数学和机械工程领域的经典数值方法,它可以用来计算结构的低阶自然频率。它是直接变分法的一种,以最小势能原理为理论基础。通过选择一个试函数来逼近问题的精确解,将试函数代入某个科学问题的泛函中,然后对泛函求驻值,以确定试函数中的待定参数,从而获得问题的近似解。
中文名:瑞利-里兹法
外文名:Rayleigh-Ritzmethod
别名:里兹法
发明时间:1877年
发明人:瑞利
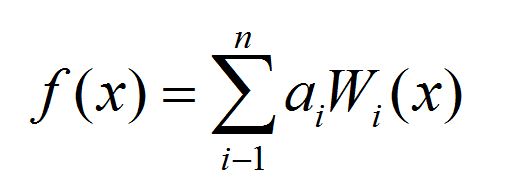
式中αi为未知常系数。通过由f(x)组成的泛函嗘
由此解出n个未知常系数αi,从而得到f(x)。这一理论还可推广到多维问题。
在求解弹性体位移时,先假定弹性体内沿x、y、z方向的位移u、v、w分别由一系列已知的满足弹性体全部位移边界条件的连续函数ui(x,y,z)、vi(x,y,z)、wi(x,y,z)(i=1,2,…,n)叠加而成,即

式中Ai、Bi、Ci为待求系数,共3n个。将u、v、w代入作为泛函的总势能Π的表达式,根据弹性学最小势能原理,总势能变分为零,即有驻值条件:
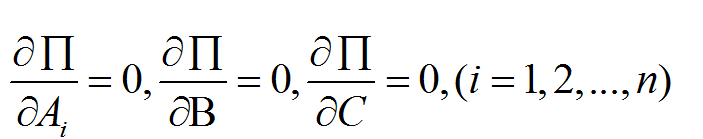
这是关于3n个待求系数Ai、Bi、Ci的3n个代数方程。解出3n个未知系数便得到全部位移。通过对位移进行微商并利用应力-应变关系就得到应力。由于瑞利-里兹法假设的位移函数u、v、w可以不满足力的边界条件,所以位移函数的构成比较容易,计算也比较方便,但有时求出的应力误差较大。
在振动问题中,如果将物体的可能位移表达为若干给定的位移的线性组合,而以瑞利商(见瑞利原理)作为位移的泛函,则利用瑞利商取驻值时条件,就可求出物体振动的固有频率的近似值。
以下的讨论举一个最简单的例子(2个集中弹簧和2个集中质量,并只考虑2个模态振型)。因此 M = 且 K = .
为该系统假设一个由两项组成的模态振型,其中一个用因数 B加权。例如Y = + B。
简谐运动理论认为挠度等于0时的速率为角频率ω乘以最大挠度(y)。本例中,每个质量的动能(KE)等于
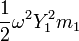
因为引入了无阻尼假设,因此整个系统当y=0时的KE等于v=0时的PE。由于不存在阻尼,系统各点同时达到v=0的状态。
因此,由KE = PE得:
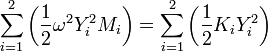
由于ω与B有关,为了找到最小的ω,我们令dω / dB = 0。此时的B的取值可以使得ω最小。由于振型是假设的,通过该方法得到的ω是需要预测的基频的上界。我们需要得到的是这个上界的最小值。
该方法有很多技巧,最重要的是试图找到尽量真实的假设振型。例如在梁的挠曲问题中,使用一个尽量接近真实解得变形模态是明智的。对于大部分简单的梁连接问题,即使振型的阶次很低,一个四次的函数就足够了。弹簧和质量并不必离散,它们可以使连续的或者是杂糅的。只要能够描述分布式的KE和PE,或把连续的单元离散,该方法可以很容易编程来找到复杂分布式系统的自然频率。
该方法可以反复迭代使用,把附加的模态振型叠加到先前的最佳解上。也可以建立一个用许多参数B和振型组合的长表达式,最后对它们求偏导。
在振动问题中,如果将物体的可能位移表达为若干给定的位移的线性组合,而以瑞利商(见瑞利原理)作为位移的泛函,则利用瑞利商取驻值的条件,就可求出物体振动的固有频率的近似值。
所以两者虽然在某个特定的条件是等效的(注意一般是用“等效”,而少用相同),但是本质是思路是不同的。
里兹法本质上和现在我们用的常用的很多有限元法是一样的,区别在于里兹法是基于全域的,而有限元是基于单元假设形函数的。很显然,基于全域的话形函数是非常难的,除非非常简单的形状,这也是为什么里兹法不能普遍的解决问题,因为它没有利用离散(离散就形函数简单,可以利用计算机的数值计算能力)。
1、本站所有文本、信息、视频文件等,仅代表本站观点或作者本人观点,请网友谨慎参考使用。
2、本站信息均为作者提供和网友推荐收集整理而来,仅供学习和研究使用。
3、对任何由于使用本站内容而引起的诉讼、纠纷,本站不承担任何责任。
4、如有侵犯你版权的,请来信(邮箱:baike52199@gmail.com)指出,核实后,本站将立即删除。





























