正态分布密度曲线反映了随机变量的分布规律。理论上的正态分布曲线是一条中间高，两端逐渐下降且完全对称的钟形曲线。

中文名：正态分布密度曲线

外文名：normal distribution curve

别名：高斯分布曲线、钟形曲线、正态曲线、正态密度曲线

组成：μ和σ2两个参数

专业：统计学

发现者：棣莫弗

应用领域：数学、物理及工程等领域

生产与科学实验中很多随机变量的概率分布都可以近似地用正态分布来描述。例如，在生产条件不变的情况下，产品的强力、抗压强度、口径、长度等指标；同一种生物体的身长、体重等指标；同一种种子的重量；测量同一物体的误差；弹着点沿某一方向的偏差；某个地区的年降水量；以及理想气体分子的速度分量，等等。一般来说，如果一个量是由许多微小的独立随机因素影响的结果，那么就可以认为这个量具有正态分布（见中心极限定理）。从理论上看，正态分布具有很多良好的性质，许多概率分布可以用它来近似；还有一些常用的概率分布是由它直接导出的，例如对数正态分布、t分布、F分布等。

表达式

参数定义

正态分布表达式中有两个参数，即期望（均数）μ和标准差σ，σ2为方差。

正态分布具有两个参数μ和σ^2的连续型随机变量的分布，第一参数μ是服从正态分布的随机变量的均值，第二个参数σ^2是此随机变量的方差，所以正态分布记作N(μ,σ2)。

μ是正态分布的位置参数，描述正态分布的集中趋势位置。概率规律为取与μ邻近的值的概率大，而取离μ越远的值的概率越小。正态分布以X=μ为对称轴，左右完全对称。正态分布的期望、均数、中位数、众数相同，均等于μ。

σ描述正态分布资料数据分布的离散程度，σ越大，数据分布越分散，σ越小，数据分布越集中。也称为是正态分布的形状参数，σ越大，曲线越扁平，反之，σ越小，曲线越瘦高。

对称性：正态曲线以均数为中心，左右对称，曲线两端永远不与横轴相交。

均匀变动性：正态曲线由均数所在处开始，分别向左右两侧逐渐均匀下降。

曲线与横轴间的面积总等于1，相当于概率密度函数的函数从正无穷到负无穷积分的概率为1。即频率的总和为100%。

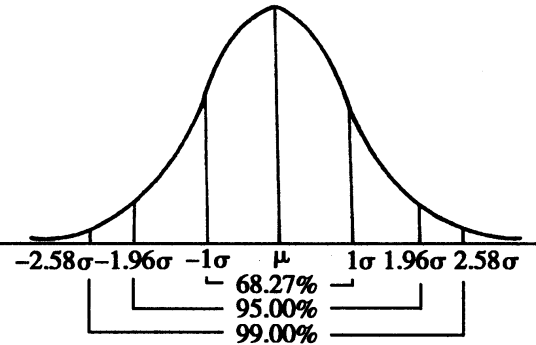
正态曲线下，横轴区间(μ-σ,μ+σ)内的面积为68.268949%。

P{|X-μ|＜σ}=2Φ(1)-1=0.6826

横轴区间(μ-1.96σ,μ+1.96σ)内的面积为95.449974%。

P{|X-μ|＜2σ}=2Φ(2)-1=0.9544

横轴区间(μ-2.58σ,μ+2.58σ)内的面积为99.730020%。

P{|X-μ|＜3σ}=2Φ(3)-1=0.9974