-
状态方程 编辑
状态方程是表征流体压强、 流体密度、 温度等三个热力学参量的函数关系式。不同流体模型有不同的状态方程。它可用下述关系表示p=p(ρT)或U=U(ρT)来表示,式中p为压强;ρ为流体密度;T为热力学温度;U为单位质量流体的内能。完全气体的状态方程为p=ρRT,式中R为气体常数;;R=287. 14m2/(s2K)。比热为常数的完全气体的状态方程为U=CvT,式中Cv为定容比热。
中文名:状态方程
外文名:state equation
公式:p=p(ρ,T)
应用领域:流体力学,包括气体、海水等
别名:物态方程
(1)理想气体的状态方程:
物质在平衡状态下p-V-T关系的数学方程。当压力足够低时,各种气体的p-V-T关系存在简单的规律。1661年,英国化学和物理学家R.玻意耳根据实验得出结论:在恒温下,一定量气体的体积与压力成反比。这一规律,后称玻意耳定律。1802年,法国化学家J.-L.盖-吕萨克发现:在恒压下一定量气体的体积与绝对温度成正比,后称盖吕萨克定律。1811年,意大利物理学家A.阿伏伽德罗提出:在恒温恒压下,同体积任何气体的摩尔数相同,后称阿伏伽德罗定律。
由这三个定律导出理想气体状态方程:pVm=RT。
式中R为摩尔气体常数,其值为8.3144J/(mol·K);p、T和Vm分别为压力、绝对温度和摩尔体积。此式亦可根据对理想气体的假设(分子间无作用力,分子本身体积可忽略),由气体分子运动理论导出。
低压下的实际气体接近于理想气体。压力升高时,实际气体的p-V-T关系都会偏离理想气体状态方程。随着化肥工业、石油化工等的发展,高压过程的应用日趋增多,促进了实际气体状态方程的研究。这种状态方程迄今已提出了几百个,但仅有十多个得到广泛应用。所有实际气体状态方程在压力趋于零时,都还原为理想气体状态方程。状态方程的研究可用理论方法和半经验方法,各自得到相应的状态方程。
就是根据分子间相互作用力的概念,由统计力学导出。式中B、C、D、……依次称为第二、三、四、……维里系数,分别反映两分子、三分子、四分子、……间的相互作用,都是温度的函数。此式适用于密度不太高的气体。对于更一般的流体,理论方程为:
式中NA为阿伏伽德罗常数;u(r)为分子间相互作用位能函数;r为分子间距;g(r)为径向分子分布函数,用以描述流体分子的分布情况。
近年来理论研究成果显著。例如:对于相互间没有吸引力的硬球分子及其混合物,已经导出比较严格的硬球状态方程。但是对于实际流体,由于对它的u(r)、g(r)两函数的具体形式尚未充分认识,还须借经验导出适用于实际流体的状态方程。
三次型方程能展开成为摩尔体积的三次式的半经验方程。这类方程比较简单,仅含两个或三个方程参数。常用的有:
范德瓦耳斯方程
J.D.范德瓦耳斯于1873年对理想气体状态方程作了修正后,提出的实际气体状态方程为:
式中α和b为物质的特征参数;
RK方程
O.雷德利克和J.N.S.于1949年在范德瓦耳斯方程的基础上提出的一个两参数方程:
它是形式最简单的常用状态方程,一般情况下有一定的准确度。式中α和b亦为物质的特征参数,由实验数据回归求取。
R方程
D.Y.彭和D.B.鲁宾逊于1976年提出如下的状态方程:
式中。此方程适用范围和SRK方程相当,在预测液体饱和体积时,其精度比SRK方程有所提高。
多参数方程 在半经验方程中,为使求解达到一定的准确度和扩大应用范围,而建立的一类比三次型方程参数更多的方程。这类方程,由于参数多,所需要的实验信息和处理数据的工作量都大为增加。应用较广的多参数方程有:
1)BWR方程
M.本尼迪克特、G.B.韦布和L.C.鲁宾于1940年提出如下的状态方程:
式中ρ=1/Vm,A0、B0、C0、α、b、c、α和γ均为特征参数,由实验数据回归而得。此方程对烃类化合物较为适用。它是第一个能同时应用于气液两相的状态方程。1970年,K.E.斯塔林对BWR方程作了改进,提出了包括11个参数的BWRS方程,应用范围比BWR方程更广。
2)马丁-侯方程
J.J.马丁和侯虞钧于1955年发表的状态方程通式如下:
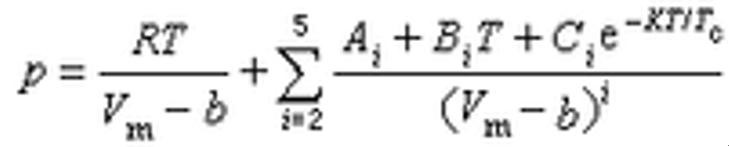 马丁-侯方程
马丁-侯方程
参数中B4=C4=A5=C5=0,其余9个参数可由临界性质(Tc,pc,Vc)和一个温度下的蒸发压数据(T0,p0)通过推导而得的公式求得。此方程原为仅适用于气相的状态方程,对烃类等非极性物质和水、氨等极性物质的气相都能适用。1981年经侯虞钧等改进后,可兼用于汽(气)液两相和混合物的汽液平衡计算。
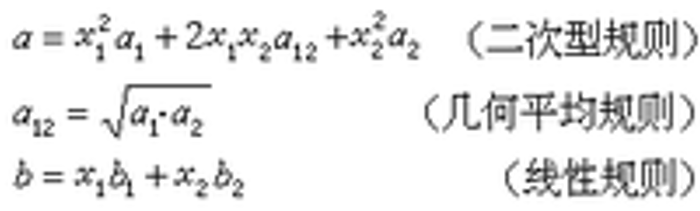 混合物状态方程
混合物状态方程
式中x表示组分的摩尔分率,下标1和2分别表示第一和第二组分。
玻意耳定律可能是第一个有关物质状态的方程表达。1662年,这位著名的爱尔兰物理学家、化学家罗伯特·波义耳利用一端封闭、管内装有气体的J形管进行了一些列实验。
查理-吕萨克定律(1787)
1787年,法国物理学家雅克·查理(Jacques Charles)发现氧气、氮气、氢气、二氧化碳和其他气体,当温度升高80开尔文(热力学温标)、其他条件一致时,气体膨胀的体积相等。
道尔顿分压定律(1801)
描述的是理想气体的特性。这一经验定律是在1801年由约翰·道尔顿所观察得到的。在任何容器内的气体混合物中,如果各组分之间不发生化学反应,则每一种气体都均匀地分布在整个容器内,它所产生的压强和它单独占有整个容器时所产生的压强相同。
理想气体定律(1834)
理想气体定律,又称理想气体状态方程,是1834年法国物理学家埃米里·克拉珀龙(法语:Benoît Paul Émile Clapeyron)综合波义耳和查里的发现得到的一个方程。
范德华方程
1873年,荷兰物理学家范德华给出了有限体积被连续分子充满情况下的物态方程。他的这一新公式改革了对于物态方程的研究。其后又有雷德利希-邝氏方程(英语:Redlich–Kwong equation of state)等对三次方程的修正。
1、本站所有文本、信息、视频文件等,仅代表本站观点或作者本人观点,请网友谨慎参考使用。
2、本站信息均为作者提供和网友推荐收集整理而来,仅供学习和研究使用。
3、对任何由于使用本站内容而引起的诉讼、纠纷,本站不承担任何责任。
4、如有侵犯你版权的,请来信(邮箱:baike52199@gmail.com)指出,核实后,本站将立即删除。





























