-
彼得森图 编辑
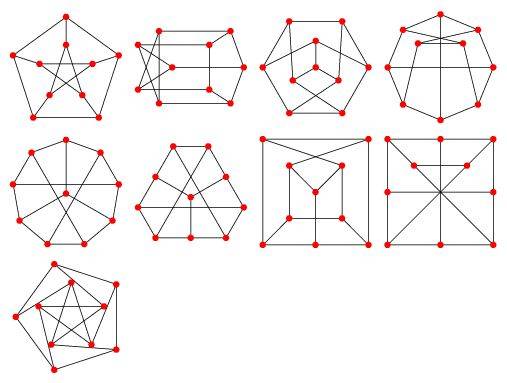
Petersen图一般译为彼得森图,是一个由10个顶点和15条边构成的连通简单图,每个点度数均为3。Petersen图的同构多种多样,其自同构有120种。它不是平面图,因而没有一种使得边与边没有交点。由于其特殊而有趣的性质,它常常被用于证明中的例子或反例。
中文名:彼得森图
外文名:Petersen graph
提出者:彼得森(Julius Petersen,1839-1910)
提出时间:1898年
适用领域:图论/组合数学
应用学科:数学
特性:常作为反例图出现
彼得森是一位出色的名教师。他讲课遇到推理困难时,总是说:“这是显而易见的”,并让学生自己查阅他的著作。同时,他是一位有经验的作家,论述问题很形象,讲究形式的优雅。
1891年,彼得森发表了一篇奠定他图论历史地位的长达28页的论文。这篇文章被公认是第一篇包含图论基本结论的文章。同时也是第一次在文章中使用“图”术语。
1898年,彼得森又发表了一篇只有3页的论文,在这篇文章中,为举反例构造了著名的彼得森图。
虽然彼得森被认为是该图的正式提出者,但实际上它最早出现于12年前,即A.B.Kempe(1886)的一篇论文中。Kempe观察到,它的顶点可以代表Desargues构型的十条线,而它的边则代表不在构型的十个点中的一个点相遇的线对。
顶点数 |V| = 10
边数 |E| = 15
分支数 ω = 1
各顶点的度为 d(v) = 3,因而它是3-正则图(立方图cubic graph)
补图为6-正则图
围长(girth) C = 5(一个图的围长是指它所包含的最短环的周长,Petersen图中无长度为3或4的环)
直径 d = 2(一个图两点间的距离指其间最短路径的长,而它的直径则指全图中最大的距离)
半径 r = 2(与距其最远点之间距离最短的点为图的中心,该距离即为图的半径)
强正则图(strongly regular graph):强正则图定义为,对于k-正则图G = (V, E),存在整数λ, μ,使得G中任意两个相邻顶点有λ个共同邻居,任意两个不相邻顶点有μ个共同邻居。对于Petersen graph,可验证(v, k, λ, μ) = (10, 3, 0, 1)。
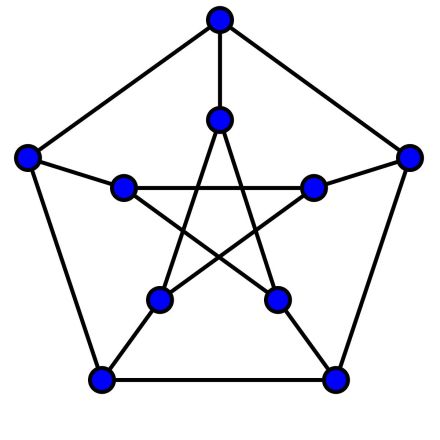 图1:Pertersen Graph
图1:Pertersen Graph
Petersen图是一个轴对称图,且其各顶点具有轮换对称性。
Petersen图与Euler图
由于Petersen图各点度数为3,显然不满足欧拉图的充要条件——连通图每点度数均为偶数。因此Petersen图不是欧拉图。
Petersen图与Hamilton图
Petersen图不是哈密尔顿图(Hamilton Graph),即不含哈密尔顿回路(Hamilton Cycle),但含240条不同的哈密尔顿路径(Hamilton Path,即经过所有点一次且仅一次的路径)。
Petersen图G满足哈密尔顿图的通常性质ω(G-S)≤|S|,即图G去除一些顶点(这些定点的集合为S)后形成的新图分支数小于等于S中顶点个数。但它并不是哈密尔顿图,从而常常作为反例出现于图论之中。
证明:Petersen图不是Hamilton图
(反证)假设Petersen图G = (V, E)是Hamilton图,其Hamilton回路为C = v1v2……v10
|E(C)| = 10,则|E(G) - E(C)| = 5,即需要为C添加5条弦才能构成原Petersen图G。接下来讨论如何添加这5条弦。
claim 1:一条弦连接的两个点在C上距离只能为4或5
(反证)由于Petersen图最小环长度为5,若C上距离1,2,3的点之间有边,会构成更小的环,矛盾;
又,C上两点最大距离为5。故一条弦连接的两个点在C上距离只能为4或5。
claim 2:至少有一条弦连接C上距离为4的两个点
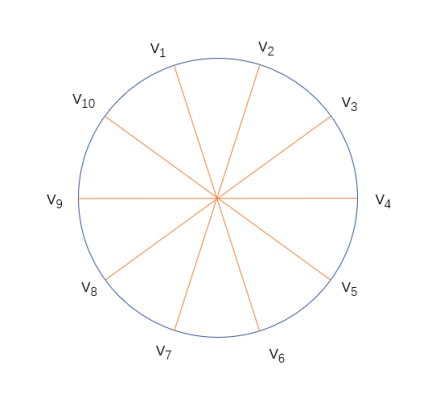 图2:5条弦均连接对侧点的情况
图2:5条弦均连接对侧点的情况
claim 3:设弦e连接C上距离为4的两个点,不失一般性设e = v1v5;则该弦两端点在上的邻居都不是弦的端点
与上同理,如果v2或v4或v10或v6连接某一条弦,则可构造出长度小于等于4的环;
综上,e = v1v5,剩下可连接弦的点有v3, v7, v8, v9,又由于G中每点度数为3,即C上每点最多连接一条弦,故最多只能再添加两条弦;与|E(G) - E(C)| = 5矛盾。原命题得证。
事实上,Petersen图是最小的亚哈密尔顿图(hypohamiltonian graph),即去掉其任意一个顶点都构成哈密尔顿图。
着色
最小点着色数(chromatic number)= 3(Petersen图是三部图),如图3。
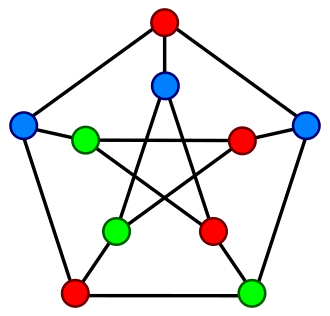 图3:Petersen图的一种3 - 点着色
图3:Petersen图的一种3 - 点着色
最小边着色数(edge chromatic number)= 4,如图4。
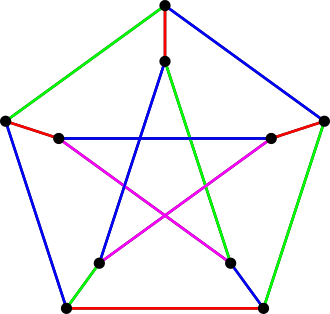 图4:Petersen图的一种4 -边着色
图4:Petersen图的一种4 -边着色
单位距离图
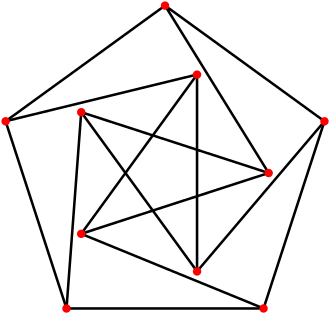 图5:Petersen图是单位距离图
图5:Petersen图是单位距离图
交叉数
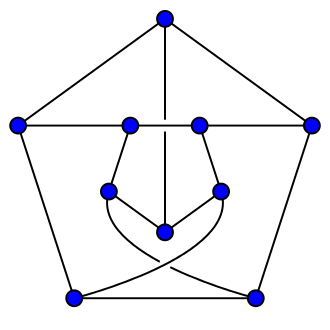 图6:Petersen图最小交叉数为2
图6:Petersen图最小交叉数为2
最小割点集
顶点连通数(vertex connectivity number)为图的最小割点集大小 。Petersen图的顶点连通数 κ(G) = 3,证明如下:
Petersen去掉任意一点,剩下的部分为Hamilton图(亚哈密尔顿图,见上);再去掉一个点至多破坏其Hamilton环获得一条Hamilton路径;再去掉第三个点,至多破坏Hamilton路径使图不连通;因此最小割点集大小至少为3。而去掉三个点确实可以使Hamilton图不连通。故其最小割点集大小为3。
最大独立集
独立数(independence number)为图的最大独立集大小 。Petersen图的最大独立集大小 α(G) = 4——我们可以分别在内层和外层找两个不相邻的顶点,得到一个大小为4的独立集;然而,如果我们想找到一个大小为5的顶点集,在外层或内层必须至少有3个顶点,而它们必然相连,故不存在大小为5的独立集。
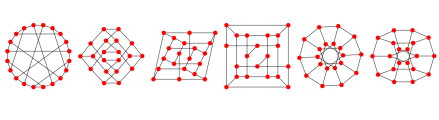 图7:Desargues图
图7:Desargues图
1、本站所有文本、信息、视频文件等,仅代表本站观点或作者本人观点,请网友谨慎参考使用。
2、本站信息均为作者提供和网友推荐收集整理而来,仅供学习和研究使用。
3、对任何由于使用本站内容而引起的诉讼、纠纷,本站不承担任何责任。
4、如有侵犯你版权的,请来信(邮箱:baike52199@gmail.com)指出,核实后,本站将立即删除。