-
波 编辑
波是指振动的传播。电磁振动的传播是电磁波。为直观起见,以绳子抖动这种最简单的为例,在绳子的一端有一个上下振动的振源,振动沿绳向前传播。从整体看波峰和波谷不断向前运动,而绳子的质点只做上下运动并没有向前运动。
中文名:波
外文名:wave
研究范畴:物理学
定义:在空间以特定形式传播的物理量
 波
波
 波
波
 波
波
各种波的共同特性还有:①在不同介质的界面上能产生反射和折射,对各向同性介质的界面,遵守反射定律和折射定律(见反射定律、折射定律);②通常的线性波叠加时遵守波的叠加原理(见光的独立传播原理);③两束或两束以上的波在一定条件下叠加时能产生干涉现象(见光的干涉);④波在传播路径上遇到障碍物时能产生衍射现象(见光的衍射);⑤横波能产生偏振现象(见光学偏振现象)。
 波
波
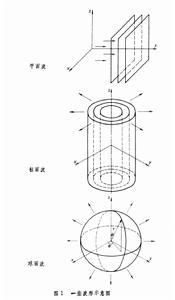
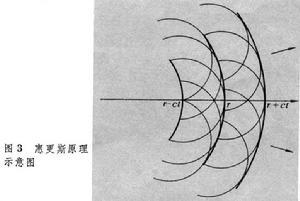
简谐振动在空间传递时形成的波动称为简谐波,其波函数为正弦或余弦函数形式。各点的振动具有相同的频率f,称为波的频率,频率的倒数为周期,即T=1/f。在波的传播方向上振动状态完全相同的相邻两个点间的距离称为波长,用λ表示,波长的倒数称波数。单位时间内扰动所传播的距离u称为波速。波速、频率和波长三者间的关系为u=fλ。波速与波的种类和传播介质的性质有关。波的振幅和相位一般是空间位置r的函数。空间等相位各点连结成的曲面称波面,波所到达的前沿各点连结成的曲面必定是等相面,称波前或波阵面。常根据波面的形状把波动分为平面波、球面波和柱面波等,它们的波面依次为平面、球面和圆柱面。实际的波所传递的振动不一定是简谐振动,而是较复杂的周期运动,称为非简谐波。任何非简谐波都可看成是由许多频率各异的简谐波叠加而成。
在波动过程中,媒质的各个质点只是在平衡位置附近振动,并不沿着振动传播的方向迁移。因此,波是振动状态的传播,不是物质本身的传播。
物理上分类:
按性质来分:主要有四种――机械波、电磁波、引力波、物质波。机械波是由扰动的传播所导致的在物质中动量和能量的传输。一般的物体都是由大量相互作用着的质点所组成的,当物体的某一部分发生振动时,其余各部分由于质点的相互作用也会相继振动起来,物质本身没有相应的大块的移动。例如,沿着弦或弹簧传播的波、声波、水波。我们称传播波的物质叫介质,它们是可形变的或弹性的和连绵延展的。对于电磁波或引力波,介质并不是必要的,传播的扰动不是介质的移动而是场——前者电磁波是电磁场在空间中以波的形式移动,引力波是时空弯曲在空间中以波的形式移动。量子力学认为,任何物质既有粒子性,又有波动性,即任何物质都具有波粒二象性,于是就有所谓的物质波(也称德布罗意波),如电子波、中子波等。
按振动方向与传播方向的关系来分:主要有三种――横波、纵波、球面波。质点振动的方向跟波的传播方向垂直的波叫横波,质点振动的方向跟波的传播方向平行的波叫纵波。
按波的形状来分:不定,波的形状象什么,就叫什么波。如方波(有的也叫矩形波)、锯齿波、脉冲波、正弦波、余弦波等。
按波长来分:长波、中波、中短波及微波。
按强度来分:常波(普通波)、冲击波。
其中在声波中还有超声波和次声波,等等,没有统一的要求,一般在什么条件下用什么分类方法。
 波
波
固体里不断发生着波动。从大的实物讲,如地球上经常出现地震波;从小的实物讲,如晶体的原子点阵间无时不在传动的点阵波。对具有特殊物理性质的固体材料,还可以激发一些特殊的波:如在压电材料里可有电声表面波;在铁磁材料里可有自旋波、磁弹波等。在等离子体里也可以激发一些不同类型的波。在地球的电离层内,由于随流体运动的磁感线对流体施加磁压,并由于流体压能够自动调整以平衡变化着的磁压,于是可以激发沿着磁感线传播的一种磁声波。这只是等离子体内可以产生的许多类型波之一。等离子气体内还可以有,例如,等离子体-电子波,等离子体-离子波等等。固体里也可以充满载流子,形成等离子体,因而可以激发一些具有特征的波,如阿
 波
波
包括光波在内的电磁波,是同人类生活关系最密切的波之一。它不仅可以在流体、固体和等离子体内传播,在真空中会照样传播。宇宙中充塞各种光和各种射电。
广义相对论还预言存在引力波,现已被实验与天文观测所证实。2016年2月11日,LIGO科学合作组织和Virgo合作团队宣布他们已经利用高级LIGO探测器,已经首次探测到了来自于双黑洞合并的引力波信号。据认为,一种较强的引力波源是双星体系。
量子力学认为,任何粒子(物质)既有粒子性,又有波动性,即任何物质都具有波粒二象性,于是就有所谓的物质波,如电子波、中子波(见波粒二象性)。波是宇宙中极广泛的现象。波的概念是物理学中少数极其重要的统一概念之一;实用上,波是信息的载体。
 波
波
 波
波
叠加性
这是波(确切地讲指线性波,见下)的一个很重要的属性。如果有两列以上的同类波在空间相遇,在共存的空间内,总的波是各个分波的矢量和(即相加时不仅考虑振幅,还考虑相位),而各个分波相互并不影响,分开后仍然保持各自的性质不变。叠加性的依据是,(线性)波的方程的几个解之和仍然是这个方程的解;这个原理称叠加原理。
干涉
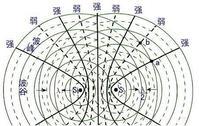 干涉图样
干涉图样
衍射
 衍射现象
衍射现象
相干性
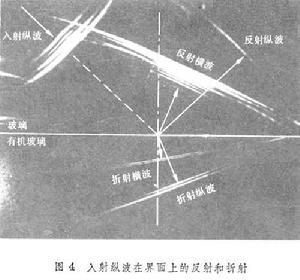
惠更斯原理:波阵面上的各点可以看作是许多子波的波源,这些子波的包络面就是下一时刻的波阵面。原理的示意图见图3(见惠更斯-菲涅耳原理)。
同干涉有关的是波的相干性。这是在激光出现前后,特别是之后,引起人们重视的一个概念。并不是任意的两列波都可以产生干涉,而需要满足一定的条件,称为相干条件,主要是要有相同的频率和固定的相位差。两个普通光源产生的光波很难产生干涉。因为光源有一定的面积,包含了许多的发光中心,而对于普通光源,这些发光中心发光时并不协调,相互间并无联系。为此,在经典的杨氏干涉实验中,有必要从同一个光源分出两束光波,以取得干涉。激光器则不然,它的多发光中心是相位关联的,它所发射的波虽还不是单频,但频带非常窄。这样,人们说普通光源所辐射的波相干性差,而激光器所辐射的则相干性好。一个波的相干性实际上是这个波能够到什么精确程度用简谐波来代表的描述。这是个定性的提法。要定量地描述相干性(严格讲是相干程度),需要用统计观点,用两点上不同时刻间扰动的时间平均。可以在一定程度上把相干性分成两个部分:一个是空间相干性,起因于光源占据有限空间;一个是时间相干性,起因于辐射波的有限频宽。
反射
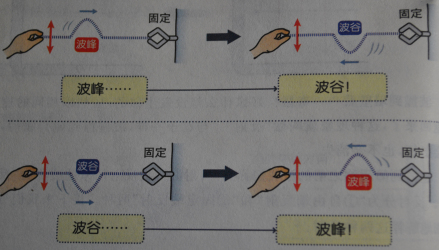 波的固定端反射
波的固定端反射
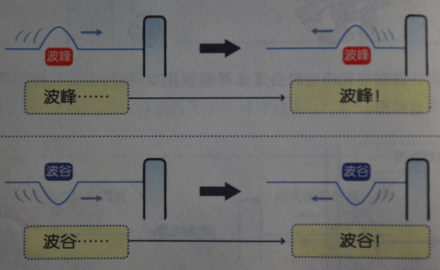 波的自由端反射
波的自由端反射
自由端反射时,反射波与入射波同相(振动状态不变);
固定端反射时,反射波与入射波异相(振动状态相反)。
反射角与入射角相等。
圆形波
波以波源(产生波的位置)为中心呈圆形向外扩展,产生圆形波。
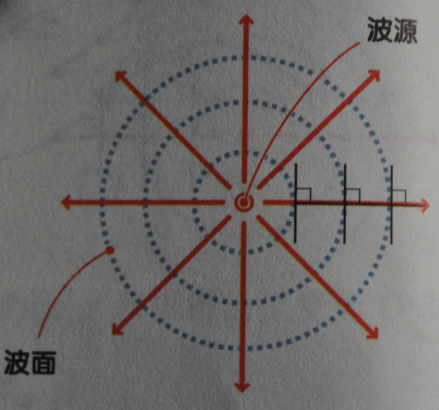 圆形波
圆形波
折射
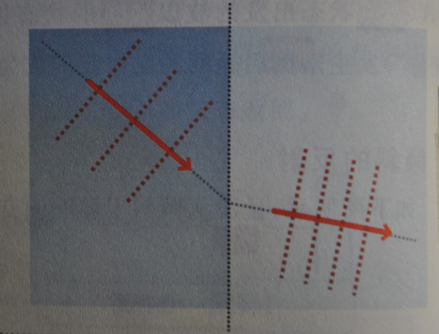 光的折射
光的折射
驻波
当连续的波在两端不断被反射时,之间产生干涉,就会停止左右运动而产生驻波。强烈振动的部分被称为波腹,完全静止的部分被称为波节。
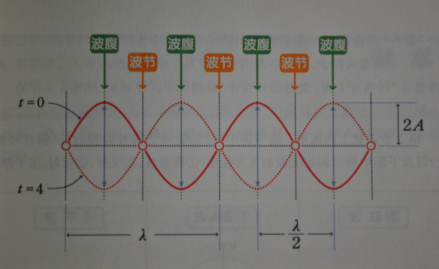 驻波
驻波
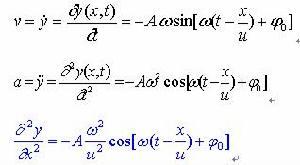 波
波
 光
光
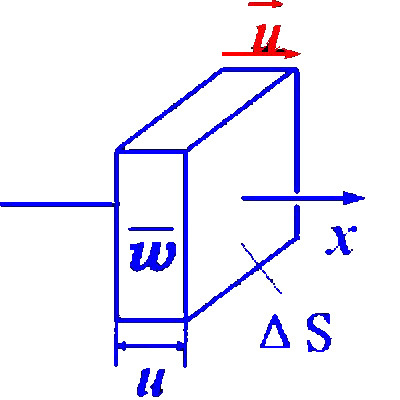
w—能量密度,所以能流为:
能流随时间周期性变化,总为正值,在一个周期内能流的平均值称为平均能流通过垂直于波动传播方向的单位面积的平均能流称为平均能流密度,通常称为能流密度或波的强度。声学中声强就是上述定义之一例。
能流密度是单位时间内通过垂直于波速方向的单位截面的平均能量。
能流密度是矢量,其方向与波速方向相同。
线性是个数学名词。因变量与自变量成正比这么一个关系叫线性关系;否则是非线性关系。波里的物理量(或其扰动)如果足够小,以致运动方程中物理量的二次项和高于二次的项,比起一次项来可以忽略不计,那么,对波的性质和行为起决定作用的,是一次项。按照线性的含意,这种波称线性波。自然界不那么简单,把一些现象限制在线性范围内。但凑巧,在许多种类的波中,人类生活中最常遇到的,正是这种用线性关系可以表达的波,如一般的(不是所有的)水波、声波、光波等。这样,在人们对波的了解过程中,首先突出了线性波。
在对于常见的波取得了一定的认识之后,人们对其他的实际波着手探讨,发现不少是非线性波。即使习见的一些波也有时是非线性的。人们用来谈话的声波是线性波。飞机以超声速运行所形成的冲击波或轰声却是非线性波。又如,大振幅电磁波在某些晶体内会产生倍频、参量振荡、参量放大等等,这就不是普通的线性电磁波所能做到的了。近年来引人重视的孤立子,是早在19世纪就注意到的非线性水波的延伸。和前面关于线性波的讨论相比,非线性波的一个突出的性质是叠加原理不成立。
为了避免涉及面太广,本条目着重讨论线性波。前面是这样做的,下面将继续这样做。
也就是说,量子力学认为物质没有确定的位置,它表现出的宏观看起来的位置其实是对几率波函数的平均值,在不测量时,它出现在哪里都有可能,一旦测量,就得到它的平均值和确定的位置。
量子力学里,不对易的力学量,比如位置和动量,是不能同时测量的,因此不能得到一个物体准确的位置和动量 ,位置测量越准 ,动量越不准。这个叫不确定性原理,当然即使不测量,它也存在。
物质波
物质波既不是机械波,也不是经典电动力学意义上的电磁波(机械波是周期性的振动在媒质内的传播,电磁波是周期变化的电磁场的传播)。在德布罗意提出物质波以后,人们曾经对它提出过各种各样的解释.到1926年,德国物理学家玻恩(1882~1970)提出了符合实验事实的后来为大家公认的统计解释:物质波在某一地方的强度跟在该处找到它所代表的粒子的几率成正比.按照玻恩的解释,物质波乃是一种几率波.德布罗意波的统计解释粒子在某处邻近出现的概率与该处波的强度成正比。
光波
根据光的波粒二象性,光波是光子在空间出现的概率波,可以通过波动的规律确定。
反射、折射和散射
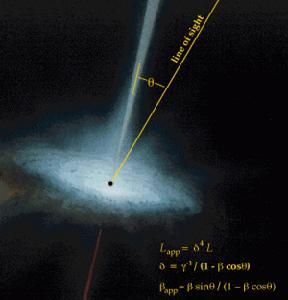
在均匀的媒质中,波沿直线传播。传播中波可能遇到新的环境。一个简单的情况是波由一种均匀的媒质射向另一种均匀媒质,而且两个媒质的界面是平面的。入射到界面的波(入射波),一部分在界面上被反射回第一媒质(称为反射波),另一部分则折入第二媒质(称为折射波)。众所周知,反射角恒等于入射角,而折射角的大小依赖于两个媒质的有关物理量的比。对于电磁波,这个物理量是介电常数同磁导率的乘积的平方根。对于其他的波有时情况要复杂些。例如,当固体中声波从一个固体媒质投射到另一固体媒质时,在第一媒质中,入射波将被反射出两个波,而不是一个,其中一个是纵波,一个是横波。进入第二媒质时也将折射出两个波(图4)。两种反射波的反射角和两种折射波的折射角都有一定的规律。
当波在传播中遇到一个实物,这时不仅出现单纯的反射和折射,还将出现其他分布复杂的波,包括衍射波。这种现象统称散射(在有些文献里,散射同衍射两个概念是不严格区分的)。用雷达追踪飞机,用声呐探寻潜艇,便属于这个情况。
行波和驻波
提起波时一般含意指不断前进的波,但在特殊情况,也可以建立起似乎囚禁在某个空间的波。为了区分,称前者为行波,称后者为驻波。
两列振幅和频率都相同,而传播方向相反的同类波叠加起来就形成驻波。常用的建立方法是让一列入射波受到媒质边界的反射,以产生满足条件的反向波,让二者叠加形成驻波。例如,简谐波在驻波腔(图5)内来回反射,驻波腔的长度是半波长的整数倍,腔端每个界面在反射时产生π相位差。驻波中振幅恒为零的点称为波节,相邻波节相距半个波长,两个波节之间的振幅按正弦形分布。振幅最大的点称为波腹。
驻波的应用也很广,如管弦乐器便利用了驻波。此外它还导出了一个重要的概念,即频率的分立。要求两个界面之间的距离d是半波长的整数倍,可以理解为,只有那些频率为n(v/2d) 的波才能建立驻波。这个频率分立的概念对量子力学的创立曾起了启发作用。
色散和群速度
在通常的媒质中,简谐波的相速度是个常数。例如,不论什么颜色的光在真空中的相速,总是恒量,等于 2.99792458×108m/s。但在某些媒质中,相速度因频率(或波长)而异。这种现象称为色散或频散。而对于非线性波,相速度还是振幅的函数。波的色散由媒质的特性决定,因此常把媒质分为色散的或非色散的。媒质会导致波的色散,一个原因是它的尺寸有限,这种色散叫位形色散。例如,在尺寸比波长大得多的固体块内,弹性波的相速度是常数,可是,对于沿直径同波长可比拟的棒面传播的弹性波,同样材料的棒便是色散的了。
媒质是色散的另一个起因在于它的内部的微观结构。有的媒质不论其形状如何,对于某些频率范围的某些种类的波总是色散的。例如,有些媒质内部的带电粒子(如电子),受入射可见光的电场激励而振动,从而反作用于这个光,导致它的色散(见电子论)。正由于水的色散性,雨后才有可能映出彩虹。
 群速度(绿)与相速度(红)的动态图解
群速度(绿)与相速度(红)的动态图解
复杂介质中传播
均匀(宏观看)而各向同性的媒质是简单的传播媒质,不少的媒质要复杂些。有些媒质是各向同性的但是不均匀。一个简单的例子是海洋中的水,由于温度、盐度、随深度而增长的压强等因素,海水带是分层的。声波的传播速度是这些因素的函数,因此随层而异,其结果是声波的传播途径远不是直线。有可能在声源前方海洋中出现没有声波的区域。比分层更不均匀的媒质,在海洋中以及在其他环境中,也是常见的。
媒质又可能是均匀但各向异性的。单晶是这类媒质。一束光射入像方解石那样的单轴晶体时,会分裂成两束光,其中一束遵守普通的折射定律,称寻常光,另一束则不遵守,称非寻常光。寻常光和非寻常光的偏振面是互相垂直的。这个现象叫双折射。同它相类似,有所谓锥形折射现象,这发生在光沿着晶体的光轴射入像霰石那样的双轴晶体时。当细束光垂直射入这样一个平块晶体,会因锥形折射而在晶体的背面出射成一圈光。可以指出,对于声波同样能观察到这样的形象。
对某些种类的媒质,有时还可以施加外场以影响和控制媒质内部的波传播。M.法拉第早在一百多年前便发现,对高折射率的各向同性材料施加强磁场,可以旋转材料中传播的光的偏振面。还可以有其他一些媒质情况,例如
不同种类的波在不同条件下的传播,在细节上是千变万化的,但在大的方面也常有类似之处。其中,日常生活中经常接触到的电磁波和(空气中)声波尤其近似,若干问题的数学处理也是互通或互相启发的。实际上在19世纪,曾经有一段时期把光看作以太的弹性波。
还有的时候,波是分散了,而不是真正的衰弱,一个例是平面波被途中许多小障碍物所折射,一部分转了向,从平面波的原来运动方向看,波的能量变小了。
同光类似,一般称为声波的声音,当波长很短时,也明显表现为粒子,称为声子。不过声子只存在于物质中,是物质振动的集体效应,与光子是不同类型的。
因此,波又有粒子性,在碰撞时遵守能量和动量守恒定律。这种情况一般发生在波与物质有相互作用时。另一方面,静止质量不为零的微观粒子,在传播时也会具有波的特性。这样扩大了波的范围。
波动方程以数学语言来表达波的特征,它给出了波函数随空间坐标和时间的变化关系。通过对带有特定的边界条件的波动方程求解,能够深入刻划波的传播规律,认识波的本质。波动方程可以分为经典的和量子力学的两类。
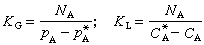 公式
公式
这里v是带有速度量纲的参量,F(r,t)是一个可观测的物理量,即波函数,r是空间坐标,t是时间,墷是拉普拉斯算符,根据需要可用不同的坐标表示。对于具体的问题,波动方程可能简化。例如,对于均匀各向同性的媒质中的点波源,波函数只同矢径有关,这时波动方程可以简化成
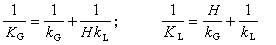 BO
BO
FC=CA
ξ(x,t)是质点位移。ξ在流体中传播的平面声波的波动方程也具有相同的形式。
FC=CA
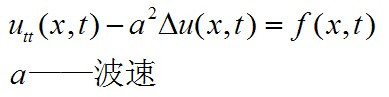 波动方程
波动方程
G=CB
E和B分别是电场强度和磁感应强度,v是相速度,在真空中v=с,是为2.99792458×108m/s的常数,在介质中v=с/n,n是介质的折射率。
1、本站所有文本、信息、视频文件等,仅代表本站观点或作者本人观点,请网友谨慎参考使用。
2、本站信息均为作者提供和网友推荐收集整理而来,仅供学习和研究使用。
3、对任何由于使用本站内容而引起的诉讼、纠纷,本站不承担任何责任。
4、如有侵犯你版权的,请来信(邮箱:baike52199@gmail.com)指出,核实后,本站将立即删除。






























