-
绝对黑体 编辑
所谓绝对黑体,就是指这样一种物体,它能够在任何温度下将辐射到它表面上的任何波长的能量全部吸收。当物体的吸收率α=1时,则表示该物体能全部吸收投射来的各种波长的热辐射线,这种物体称为绝对黑体,或简称黑体(black body)。黑体是对热辐射线吸收能力最强的一种理想化物体,实际物体没有绝对黑体。但在理论研究中可设计种种绝对黑体。例如:设有一个空心容器,器壁由不透明材料制成,器壁上开有一个小孔,这样即可构成一个黑体。因为当射线射入小孔后,将在空腔中进行多次反射,每次反射器壁的内表面就吸收一部份能量,若小孔孔径开得很小,远远小于容器的表面积。这样,射线即可认为被小孔全部吸收。小孔就可认为是绝对黑体。绝对黑体的发射率也为1。
目录
中文名:绝对黑体
外文名:absolute black body
特点:投射的辐射热全被该物体吸收
简称:黑体
理论黑体:现实中没有绝对黑体
领域:物理
绝对黑体的吸收率
一般物体收到辐射时,对辐射能量总是有吸收、有反射。吸收部分占总能量的份额称为吸收率,其值在0-1之间。黑颜色的物体吸收能力大于白颜色的物体,吸收系数也比较大。如果吸收系数为1,表示全部能量都被吸收而没有反射。具有这种能力的物体称为绝对黑体。自然界并不存在绝对黑体。绝对黑体是一个理想化的参考模型。
绝对黑体与温度
在遥感热红外扫描仪系统中,装有高温黑体和低温黑体,作为探测地物热辐射的参考源。实用的绝对黑体是由人工方法制成的。一般说,物体的辐射能量与其表面温度有关,温度越高,辐射能量越大。换句话说,物体的辐射能随其温度变化,辐射能的光谱分布也随之变化。
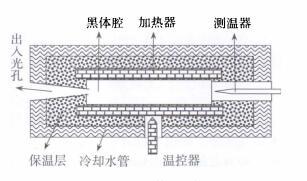 图1 黑体的结构
图1 黑体的结构
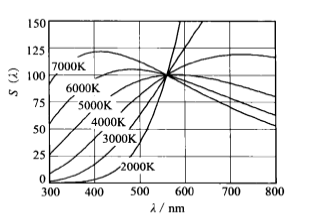 图2 黑体的光谱能量分布
图2 黑体的光谱能量分布
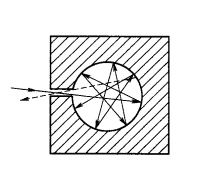 图3 带有小孔的空腔
图3 带有小孔的空腔
后,再由容器小孔O射出容器外的能量将为
如果把空心容器的内腔的腔壁加热,并让其保持在一定的温度T,则由小孔内向外的辐射可以认为是绝对黑体在温度为T时的辐射。换句话说,由小孔射出的辐射,相当于从面积等于小孔面积,温度为T的绝对黑体表面所射出。
在常温下,所有物体的辐射都很弱,黑色物体或空腔小孔的反射又极少,所以看起来它们就很暗,例如,白天看建筑物的窗口时,窗口看起来很黑,就是这个道理。但是,在高温下,黑体的辐射最强,故看起来它们最明亮。%20
1.普朗克黑体辐射方程
黑体的光谱面辐射度(W/m2)为
Rλ=2πc2h/%20(1a)
式中:λ——波长(m);
h——普朗克常数(=6.626%20075%205×10-34%20J·s);
c——真空中的光速(=3×108%20m/s);
k——玻耳兹曼常数(=1.380%20658×10-23%20J/K);
T——绝对温度(K)。
由于黑体是朗伯辐射源,其面辐射度R=Lλ·π,所以,黑体辐射亮度
Lλ=2c2h/%20(1b)
2.瑞利一琴斯定律
对于hv=hc/λ《kT,即黑体温度较高,或波长较长时,由式(1b)可导出瑞利一琴斯定律:%20
Lλ≈2kTν2/c2(2)
式(2)在理解3~5μm、8~12μm红外成像评价理论时有实际意义。此时,在既定温度(T)下,目标的亮度(%20Lλ)与其亮度对比度和温差对比度具有同样的量纲和随大气距离衰减的类似规律,图4所示是绝对黑体辐射亮度光谱分布曲线。
3.斯蒂芬一玻耳兹曼方程
该方程给出黑体辐射的所有波长的总面辐射度R,即
R=
式中:σ——斯蒂芬一玻耳兹曼常数,其值为2π5k4/(15h3c2)。
式(3)的物理意义说明,绝对黑体的总面辐射度与温度的四次方成正比。
4.维恩位移定律
该定律给出黑体辐射光谱峰值面辐射度所对应的波长λm与其温度T的关系。可以证明
λmT=2 898μm·K(4)
这说明,黑体温度越高,其辐射峰值波长越移向短波。人们仔细观察火焰时不难发现,随着火焰温度的升高,其颜色将按红一黄一绿一蓝规律变化。虽说火焰不是黑体,但现象是类似的。
1、本站所有文本、信息、视频文件等,仅代表本站观点或作者本人观点,请网友谨慎参考使用。
2、本站信息均为作者提供和网友推荐收集整理而来,仅供学习和研究使用。
3、对任何由于使用本站内容而引起的诉讼、纠纷,本站不承担任何责任。
4、如有侵犯你版权的,请来信(邮箱:baike52199@gmail.com)指出,核实后,本站将立即删除。