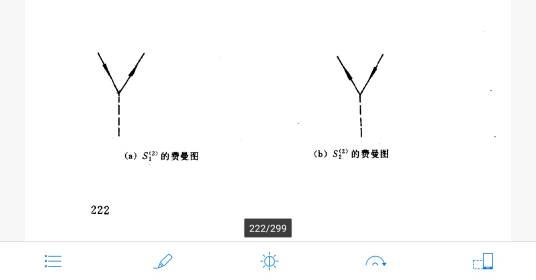
-
费曼图 编辑
中文名:费曼图
外文名:Feynman diagram
定义:第三种量子力学的方式
作用:广泛运用于统计学
应用学科:量子力学术语
范畴:理工科
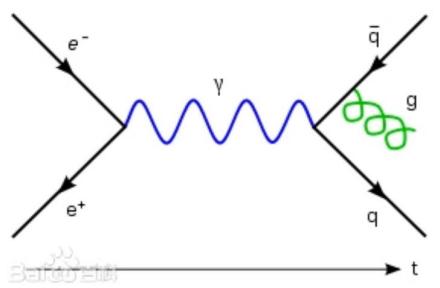 费曼图
费曼图
但是,作为摄动的展开式,费曼图不能包涵非摄动效应。
除了它们在作为数学技巧的价值外,费曼图为粒子的相互作用提供了深入的科学理解。粒子会在每一个可能的方式下相互作用:实际上,居间的虚粒子超越光速是允许的。(这是基于测不准原理,并且不违反相对论,因为狭义相对论只要求可观测量满足因果律;事实上,超越光速对保留相对性时空的偶然性有帮助。)每一个终态的概率然后就从所有如此的概率中得出。这跟量子力学的功能积分表述有密切关系,该表述(路径积分)也是由费曼发明的。
如此计算如果在缺少经验的情况下使用,通常会得出图的振幅为无穷大,这个答案在物理理论中是要不得的。问题在于粒子自身的相互作用被错误地忽视了。重整化的技巧(是由费曼、施温格和朝永所开发的)弥补了这个效应并消除了麻烦的无穷大项。经过这样的重整化后,用费曼图做的计算通常能与实验结果准确地吻合。
费曼图及路径积分法亦被应用于统计力学中。
有关费图及路径积分的数学内容尚未完善,它还处于依赖物理直观的阶段。
1、本站所有文本、信息、视频文件等,仅代表本站观点或作者本人观点,请网友谨慎参考使用。
2、本站信息均为作者提供和网友推荐收集整理而来,仅供学习和研究使用。
3、对任何由于使用本站内容而引起的诉讼、纠纷,本站不承担任何责任。
4、如有侵犯你版权的,请来信(邮箱:baike52199@gmail.com)指出,核实后,本站将立即删除。