-
突变论 编辑
突变论是研究自然界和人类社会中连续渐变如何引起突变或飞跃,并力求以统一的数学模型来描述,预测并控制这些突变或飞跃的一门学科。它把人们关于质变的经验总结成数学模型,表明质变既可通过飞跃的方式,也可通过渐变的方式来实现,并给出了两种质变方式的判别方法,它还表明,在一定情况下,只要改变控制条件,一个飞跃过程可以转化为渐变,而一个渐变过程又可转化为飞跃。突变论认为事物结构的稳定性是突变论的基础,事物的不同质态从根本上说就是一些具有稳定性的状态,这就是为什么有的事物不变,有的渐变,有的则突变的内在原因。在严格控制条件的情况下,如果质变经历的中间过渡状态是不稳定的,它就是一个飞跃过程; 如果中间状态是稳定的,它就是一个渐变过程。
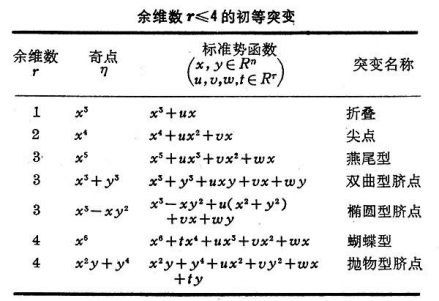
突变论是一门着重应用的科学,它既可以用在“硬”科学方面,又可以用于“软”科学方面。在数学上突变论属于微分流形拓扑学的一个分支,是关于奇点的理论。它可以根据势函数而把临界点分类,并且研究各种临界点附近的非连续现象的特征。
 突变论
突变论
因为英文 catastrophe一词的原意为突然来临的灾祸,所以也有把它译作灾变论。突变论一般并不给出产生突变机制的假设,而是提供一个合理的数学模型来描述现实世界中产生的突变现象,对它进行分类,使之系统化。突变论特别适用于研究内部作用尚属未知、但已观察到有不连续现象的系统。
后来突变论被重新定义和提出,它是20世纪60年代末法国数学家R.托姆为了解释胚胎学中的成胚过程而提出来的。1967年托姆发表《形态发生动力学》一文,阐述突变论的基本思想,1969年发表《生物学中的拓扑模型》,为突变论奠定了基础。1972年发表专著《结构稳定与形态发生》,系统地阐述了突变论。70年代以来,E.C.塞曼等人提出著名的突变机构,进一步发展了突变论,并把它应用到物理学、生物学、生态学、医学、经济学和社会学等各个方面,产生了很大影响。
 突变论
突变论
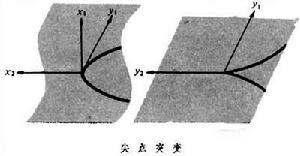
1955年H·惠特尼在研究这种映射的特点时,得出两类一般奇点。一类是折叠,可用公式y1=x剐,y2=x2表示。把球面投射到平面上,赤道上的点产生的奇点就是这种奇点。另一类是尖点,局部坐标可写成y1=x劅+x1x2,y2=x2。把空间曲面y1=x劅+x1x2投影到平面(y1,y2)上,平面上有一半立方抛物线,在原点处有一个尖点 (见图)。曲线把平面分成两部分,较小部分的原像均由三点构成,而较大部分只由一个点构成。在尖点处映射引起突变,这是突变论所研究的最常见的一种突变。
惠特尼证明,尖点是稳定的,也就是在这种映射附近的映射在适当的地方也有同类的奇点。
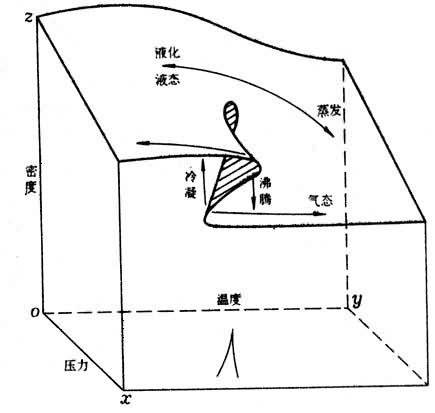
突变论认为,系统所处的状态,可用一组参数描述。当系统处于稳定态时,标志该系统状态的某个函数就取唯一的值。当参数在某个范围内变化,该函数值有不止一个极值时,系统必然处于不稳定状态。雷内托姆指出:系统从一种稳定状态进入不稳定状态,随参数的再变化,又使不稳定状态进入另一种稳定状态,那么,系统状态就在这一刹那间发生了突变。突变论给出了系统状态的参数变化区域。
突变论提出,高度优化的设计很可能有许多不理想的性质,因为结构上最优,常常联系着对缺陷的高度敏感性,就会产生特别难于对付的破坏性,以致发生真正的“灾变”。在工程建造中,高度优化的设计常常具有不稳定性,当出现不可避免的制造缺陷时,由于结构高度敏感,其承载能力将会突然变小,而出现突然的全面的塌陷。突变论不仅能够应用于许多不同的领域,而且也能够以许多不同的方式来应用。
通过突变论能够有效地理解物质状态变化的相变过程,理解物理学中的激光效应,并建立数学模型。通过初等突变类型的形态可以找到光的焦散面的全部可能形式。应用突变论还可以恰当地描述捕食者----被捕食者系统这一自然界中群体消长的现象。过去用微积分方程式长期不能满意解释的,通过突变论能使预测和实验结果很好地吻合。突变论还对自然界生物形态的形成作出解释,用新颖的方式解释生物的发育问题,为发展生态形成学作出了积极贡献。
突变论对哲学上量变和质变规律的深化,具有重要意义。很长时间以来,关于质变是通过飞跃还是通过渐变,在哲学上引起重大争论,历史上形成三大派观点:“飞跃论”、“渐进论”和“两种飞跃论”。突变论认为,在严格控制条件的情况下,如果质变中经历的中间过渡态是稳定的,那么它就是一个渐变过程。质态的转化,既可通过飞跃来实现,也可通过渐变来实现,关键在于控制条件。
应用突变论还可以设计许许多多的解释模型。例如经济危机模型,它表现经济危机在爆发时是一种突变,并且具有折迭型突变的特征,而在经济危机后的复苏则是缓慢的,它是经济行为沿着“折迭曲面”缓慢滑升的渐变。此外,还有“社会舆论模型”、“战争爆发模型”、“人的习惯模型”、“对策模型”、“攻击与妥协模型”等等。
突然现象
突变论能解说和预测自然界和社会上的突然现象,无疑它也是软科学研究的重要方法和得力工具之一。突变论在数学、物理学、化学、生物学、工程技术、社会科学等方面有着广阔的应用前景。《大英百科年鉴》1977年版中写道:“突变论使人类有了战胜愚昧无知的珍奇武器,获得了一种观察宇宙万物的深奥见解”。
自然,突变论的应用在某些方面还有待进一步的验证,在将社会现象全部归结为数学模型来模拟时还有许多技术细节要解决,在参量的选择和设计模型方面还有大量工作要做。此外,突变理论本身也还有待于进一步完善,在突变论的方法上也有许多争议之处。
总之,突变论问世以来,引起褒贬不一的评述,正象任何一门新兴学科的发展经历一样。著名数学家斯图尔特客观地评价了突变论,他写道:“适当地理解突变理论,可以为我们生存的世界提供新颖而深入的见解。但它还需要加以发展、检验、修改,经历一般成为可靠的科学工具的全部过程。但我毫不怀疑,也不是宇宙中的唯一事物”。
突变论在许多领域已经取得了重要的应用成果。随着研究的深入,它的应用范围在不断扩大,相信它在我国四化建设中将发挥重要作用。
1、本站所有文本、信息、视频文件等,仅代表本站观点或作者本人观点,请网友谨慎参考使用。
2、本站信息均为作者提供和网友推荐收集整理而来,仅供学习和研究使用。
3、对任何由于使用本站内容而引起的诉讼、纠纷,本站不承担任何责任。
4、如有侵犯你版权的,请来信(邮箱:baike52199@gmail.com)指出,核实后,本站将立即删除。