-
牛顿第二运动定律 编辑
牛顿第二运动定律(Newton's Second Law of Motion-Force and Acceleration)的常见表述是:物体加速度的大小跟作用力成正比,跟物体的质量成反比,且与物体质量的倒数成正比;加速度的方向跟作用力的方向相同。该定律是由艾萨克·牛顿在1687年于《自然哲学的数学原理》一书中提出的。牛顿第二运动定律和第一、第三定律共同组成了牛顿运动定律,阐述了经典力学中基本的运动规律。
动量为
常见表述:
物体加速度的大小与合外力成正比,与物体质量成反比(与物体质量的倒数成正比)。加速度的方向与合外力的方向相同。牛顿第二运动定律可以用比例式来表示,即
瞬时性:牛顿第二运动定律是力的瞬时作用效果,加速度和力同时产生、同时变化、同时消失。
矢量性:
独立性:物体受几个外力作用,在一个外力作用下产生的加速度只与此外力有关,与其他力无关,各个力产生的加速度的矢量和等于合外力产生的加速度,合加速度和合外力有关。
因果性:力是产生加速度的原因,加速度是力的作用效果。故力是改变物体运动状态的原因。
等值不等质性:虽然
牛顿第二运动定律验证实验,就是测量在不同的
利用现代的实验教学设施改进和补充原来的实验手段,更能体现出物理学的科学素养和科学态度。%20
在气垫导轨上验证: 将气垫导轨调平后(由于导轨都存在一定的弯曲,滑块与导轨间存在阻力,所以调平在实验中一般用滑块通过两个光电门时的速度相等来衡量),测出粘性阻尼常数b。 为了修正粘滞性摩擦阻力的存在所引起的速度损失,必须解决粘滞性阻尼常数的测定问题。其方法主要有以下两种:倾斜导轨法、振动法。 |
|
用非线性回归法验证: 在气垫导轨上验证定律影响测量的主要因素是空气阻力,通过修正可将影响减小到可忽略的程度。但常采用的一元线性回归法,不足以说明整个回归方程的好坏;二元线性回归法也同样存在一定的问题。 用非线性回归法验证定律,首先对质点运动的动力学模型进行线性化处理,得到模型的参数线性估计值,并以其作为非线性模型的初值对动力学模型进行非线性回归分析。非线性回归法验证了定律的正确性,改进了验证定律的传统实验方法,具有一定的应用和推广价值。 |
|
此外,验证牛顿第二运动定律还有基于LabVIEW的教学平台、基于无线模块和Visual Basic的仿真演示实验设计、基于光电传感器的实验装置。
牛顿第二运动定律只适用于惯性参考系。惯性参考系是指牛顿运动定律成立的参考系,在非惯性参考系中牛顿第二运动定律不适用。但是,通过惯性力的引入。可以使牛顿第二运动定律的表示形式在非惯性系中使用。
牛顿第二运动定律只适用宏观问题。解决微观问题必须使用量子力学。当考察物体的运动线度可以和该物体的德布罗意波相比拟时,由于粒子运动不确定性关系式(即无法同时准确测定粒子运动的方向与速度),物体的动量和位置已经是不能同时准确获知的量了,因而牛顿动力学方程缺少准确的初始条件无法求解。也就是说经典的描述方法由于粒子运动不确定性关系式已经失效或者需要修改。量子力学用希尔伯特空间中的态矢概念代替位置和动量(或速度)的概念(即波函数)来描述物体的状态,用薛定谔方程代替牛顿动力学方程(即含有力场具体形式的牛顿第二运动定律)。用态矢代替位置和动量的原因是由于测不准原理我们无法同时知道位置和动量的准确信息,但是我们可以知道位置和动量的概率分布,测不准原理对测量精度的限制就在于两者的概率分布上有一个确定的关系。
牛顿第二运动定律只适用低速问题。解决高速问题必须使用相对论。由于牛顿动力学方程不是洛伦兹协变的,因而不能和狭义相对论相容,因此当物体做高速移动时需要修改力、速度等力学变量的定义,使动力学方程能够满足洛伦兹协变的要求,在物理预言上也会随速度接近光速而与经典力学有不同。
艾萨克·牛顿把这一假定作为牛顿第一运动定律,并将伽利略的思想进一步推广到有力作用的场合,提出了牛顿第二运动定律。
1684年8月起,在埃德蒙多·哈雷的劝说下,牛顿开始写作《自然哲学的数学原理》,系统地整理手稿,重新考虑部分问题。1685年11月,形成了两卷专著。1687年7月5日,《原理》使用拉丁文出版。《原理》的绪论部分中的运动的公理或定律一节中提出了牛顿第二运动定律。
运用牛顿第二定律及同一直线矢量合成方法,根据理想“平行导轨模型”的物理特点,基于电磁感应规律,对电磁感应中的电容负载平行导轨模型的各种情况进行计算,可计算出各种情况下的金属导杆运动的数学表达式;结果与实践吻合。
动画是让画面运动起来的影视艺术,即运动的画面。牛顿第二运动定律在动画艺术中占有重要的位置,是动画中必不可少的研究对象。
牛顿第二运动定律定量地说明了物体运动状态的变化和对它作用的力之间的关系,和牛顿第一运动定律、牛顿第三运动定律共同组成了牛顿运动定律,是力学中重要的定律,是研究经典力学的基础阐述了经典力学中基本的运动规律。
1、本站所有文本、信息、视频文件等,仅代表本站观点或作者本人观点,请网友谨慎参考使用。
2、本站信息均为作者提供和网友推荐收集整理而来,仅供学习和研究使用。
3、对任何由于使用本站内容而引起的诉讼、纠纷,本站不承担任何责任。
4、如有侵犯你版权的,请来信(邮箱:baike52199@gmail.com)指出,核实后,本站将立即删除。
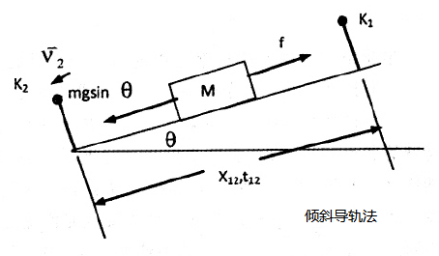 倾斜导轨法
倾斜导轨法 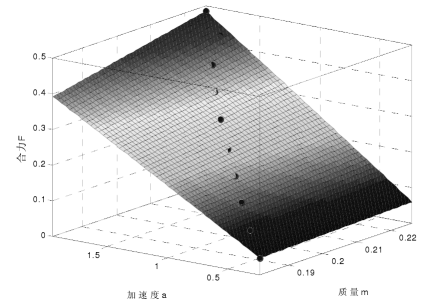 牛顿第二运动定律非线性拟合图
牛顿第二运动定律非线性拟合图 




























