-
重力加速度 编辑
重力加速度,物理学名词。重力对自由下落的物体产生的加速度,称为重力加速度。如果以m表示物体的质量,以g表示重力加速度,重力G可表示为G=mg。重力加速度是地球物理研究中的一个基本矢量,也是对一般力学系统进行力学分析时需要考虑的一个重要参数。在对精度要求不是很高的情况下,将其作为常量处理所带来的误差较小时,重力异常可以忽略不计,并可在一定程度上减少计算量。
重力加速度是矢量,它的方向总是竖直向下的,它的大小可以用实验方法求出。实验证明:重力加速度的大小随其在地球上地点的不同而略有差异。例如在赤道上g=9.780 m/s2,在北极g=9.832 m/s2,在北纬45°的海平面上g=9.807 m/s2,在北京g=9.801 m/s2等。通常在没有明确说明的时候g取9.80 m/s2。在进行粗略的计算或有说明时可以把g取作10m/s2 。
在地球上同一地点,重力加速度是一个恒定的矢量。这就决定了自由落体运动实质上是一个初速度为零的匀加速直线运动 。
式中:g为重力加速度;G,M为与地球质量有关的常数;r为地球中心至计算点的距离或半径%20。
上面的方程给出了重力加速度的大小,其作用方向是沿导弹与地球中心间连线的方向。这里要注意的关键是,了解位置才能求得重力加速度,而且其大小与半径的平方成反比,它随高度的增大而迅速减小%20。
距离地面同一高度的重力加速度,也会随着纬度的升高而变大。由于重力是万有引力的一个分力,万有引力的另一个分力提供了物体绕地轴作圆周运动所需要的向心力。物体所处的地理位置纬度越高,圆周运动轨道半径越小,需要的向心力也越小,重力将随之增大,重力加速度也变大。地理南北两极处的圆周运动轨道半径为0,需要的向心力也为0,重力等于万有引力,此时的重力加速度也达到最大%20。
通常指地面附近物体受地球引力作用在真空中下落的加速度,记为g。为了便于计算,其近似标准值通常取为980cm/s2或9.8m/s2。在月球、其他行星或星体表面附近物体的下落加速度,则分别称月球重力加速度、某行星或星体重力加速度%20。
在近代一些科学技术问题中,须考虑地球自转的影响。更精确地说,物体下落的加速度g是由地心引力和地球自转引起的惯性离心力的合力产生的。由于地球是微椭球体,又有自转,所以重力加速度的方向一般不通过地心。重力加速度的测定,对物理学、地球物理学、重力探矿、空间科学等都具有重要意义%20。
地球上几个不同纬度处的g值见下表;从中可以看出g值随纬度的变化情况:
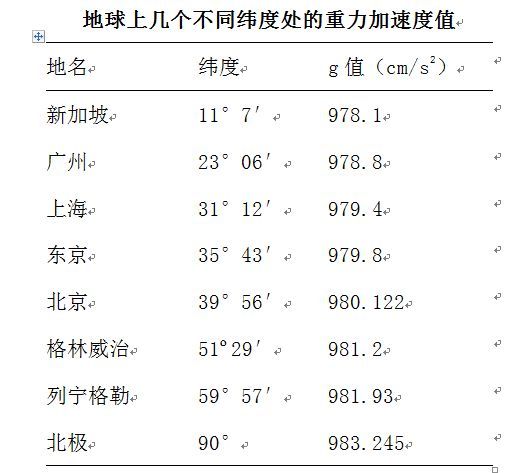 不同地区的重力加速度值
不同地区的重力加速度值
由于地球是微椭球形的,加之有自转,在一般情况下,重力加速度的方向不通过地心,重力加速度的测定,对物理学、地球物理学、重力探矿、空间科学等都具有重要意义 。
纬度 | 重力加速度 | 纬度 | 重力加速度 |
0 | 9.78030 | 30 | 9.79321 |
10 | 9.78186 | 40 | 9.80166 |
20 | 9.78634 | 50 | 9.81066 |
60 | 9.81914 | 80 | 9.83058 |
70 | 9.82606 | 90 | 9.83218 |
不同高度的重力加速度 (单位: m/s2)
海拔 (km) | 纬度(度) | |||||||||
0 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | |
0 | 9.780 | 9.782 | 9.786 | 9.793 | 9.802 | 9.811 | 9.819 | 9.826 | 9.831 | 9.832 |
4 | 9.768 | 9.770 | 9.774 | 9.781 | 9.789 | 9.798 | 9.807 | 9.814 | 9.818 | 9.820 |
8 | 9.756 | 9.757 | 9.762 | 9.768 | 9.777 | 9.786 | 9.794 | 9.801 | 9.806 | 9.807 |
12 | 9.743 | 9.745 | 9.749 | 9.756 | 9.765 | 9.774 | 9.782 | 9.789 | 9.794 | 9.795 |
16 | 9.731 | 9.732 | 9.737 | 9.744 | 9.752 | 9.761 | 9.770 | 9.777 | 9.781 | 9.783 |
20 | 9.719 | 9.720 | 9.725 | 9.732 | 9.740 | 9.749 | 9.757 | 9.764 | 9.769 | 9.770 |
 离心力公式
离心力公式
m为物体的质量;ω为地球自转的角速度;
在高度为H的重力加速度g(1930年国际重力公式)同H和
式中H为以米为单位的数值 。
 重力及重力加速度的方向
重力及重力加速度的方向
地球物理学研究中要求观测重力长规的细微的变化,即所谓g的长度;这种变化可能是由于地壳运动,地球的内部结构和形状的演变,太阳系中动力常数的长度以及引力常数G的变化等等。观测这些变化要求g值的计量不确定度达10-8至10-9量级。观测g值的变化可能对预报地震有密切的关系,据有关方面报道,七级地震相对应的g值变化约为0.1×10-5m/s2。目前,许多国家都在探索用g值的变化作临重力加速度的测量震预报 。
重力探矿是利用地下岩石和矿体密度的不同而引起地面重力加速度的相应的变化。故根据在地面上或海上测定g的变化,就可以间接地了解地下密度与周围岩石不同的地质构造、矿体和岩体埋藏情况,圈定它们的位置 。
1、本站所有文本、信息、视频文件等,仅代表本站观点或作者本人观点,请网友谨慎参考使用。
2、本站信息均为作者提供和网友推荐收集整理而来,仅供学习和研究使用。
3、对任何由于使用本站内容而引起的诉讼、纠纷,本站不承担任何责任。
4、如有侵犯你版权的,请来信(邮箱:baike52199@gmail.com)指出,核实后,本站将立即删除。






























