-
19 编辑
19
19（十九）是18与20之间的自然数。属于奇数、质数。是一个阿拉伯数字。为正整数。数论中19是Heegner数。
中文名：十九
外文名：nineteen
别名：19
罗马数字：XIX
二进制：10011
三进制：201
四进制：103
八进制：23
十二进制：17
十六进制：13
倒数循环节：18位
第20个自然数。
第19个正整数。
第8个素数。前一个为17、下一个为23。
第4对孪生素数之一（17，19）。
第8个陈素数。
第7个瓦格斯塔夫质数。
第5个危险素数。前一个是17、下一个是29。
十进制下，既非可右截短质数，也非可左截短质数。
四胞胎素数组合（n，n+2，n+6，n+8）之一（11，13，17，19）；下一个组合为（101，103，107，109）
高斯质数之一。
第16个亏数，真约数和为1，亏度为18。前一个为17、下一个为21。
第12个不寻常数，大于平方根的素因数为19。前一个为17、下一个为20。
第13个无平方数因数的数。前一个为17、下一个为21。
第13个十进制的等数位数。前一个为17、下一个为21。
第4个中心三角形数。
第3个中心的六边形数。
第3个八面体数。
第7个梅森质数（
循环单位1 111 111 111 111 111 111是质数。
每个正整数是最多19个4次方之和（华林问题）。
基思数。
第5个快乐数：19→1²+9²=82→8²+2²=68→6²+8²=100→1²+0²+0²=1。
倒数：
神奇之处
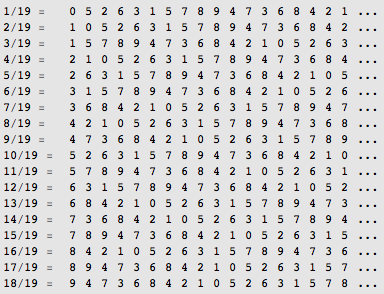19x19的方阵
答案是，它是一个幻方——每一行、每一列和两条对角线上的数字之和都是 81 （注：严格意义上说它不算幻方，因为有相同数字）。
倍数表
乘数 | 乘积 |
|---|---|
1 | 19 |
2 | 38 |
3 | 57 |
4 | 76 |
5 | 95 |
6 | 114 |
7 | 133 |
8 | 152 |
9 | 171 |
10 | 190 |
11 | 209 |
12 | 228 |
13 | 247 |
14 | 266 |
15 | 285 |
16 | 304 |
17 | 323 |
18 | 342 |
19 | 361 |
20 | 380 |
21 | 399 |
22 | 418 |
23 | 437 |
24 | 456 |
25 | 475 |
26 | 494 |
27 | 513 |
28 | 532 |
29 | 551 |
30 | 570 |
31 | 589 |
32 | 608 |
33 | 627 |
…… | |
次方表
次方 | 次方数 |
|---|---|
1 | 19 |
2 | 361 |
3 | 6,859 |
4 | 130,321 |
5 | 2,476,099 |
6 | 47,045,881 |
7 | 893,871,739 |
8 | 16,983,563,041 |
9 | 322,687,697,779 |
10 | 6,131,066,257,801 |
11 | 116,490,258,898,219 |
12 | 2,213,314,919,066,161 |
13 | 42,052,983,462,257,059 |
14 | 799,006,685,782,884,121 |
15 | 15,181,127,029,874,798,299 |
16 | 288,441,413,567,621,167,681 |
17 | 5,480,386,857,784,802,185,939 |
18 | 104,127,350,297,911,241,532,841 |
19 | 1,978,419,655,660,313,589,123,979 |
20 | 37,589,973,457,545,958,193,355,601 |
21 | 714,209,495,693,373,205,673,756,419 |
22 | 13,569,980,418,174,090,907,801,371,961 |
23 | 257,829,627,945,307,727,248,226,067,259 |
24 | 4,898,762,930,960,846,817,716,295,277,921 |
25 | 93,076,495,688,256,089,536,609,610,280,499 |
…… | |
钾的原子序数
一般的围棋比赛都使用19路棋盘。
在特定情况下作为学号。
1、本站所有文本、信息、视频文件等，仅代表本站观点或作者本人观点，请网友谨慎参考使用。
2、本站信息均为作者提供和网友推荐收集整理而来，仅供学习和研究使用。
3、对任何由于使用本站内容而引起的诉讼、纠纷，本站不承担任何责任。
4、如有侵犯你版权的，请来信（邮箱:baike52199@gmail.com）指出，核实后，本站将立即删除。
