2.把不规则的图形转化为规则的图形，把复杂图形转化为简单的基本图形。

3.平面几何中，辅助线用虚线表示。立体几何中，看得见的用实线表示，看不见的用虚线表示。

三角形问题

方法1：有关三角形中线的题目，常将中线加倍。含有中点的题目，常常利用三角形的中位线，通过这种方法，把要证的结论恰当的转移，很容易地解决了问题。

方法2：含有平分线的题目，常以角平分线为对称轴，利用角平分线的性质和题中的条件，构造出全等三角形，从而利用全等三角形的知识解决问题。

方法3：结论是两线段相等的题目常画辅助线构成全等三角形，或利用关于平分线段的一些定理。

方法4：结论是一条线段与另一条线段之和等于第三条线段这类题目，常采用截长法或补短法，所谓截长法就是把第三条线段分成两部分，证其中的一部分等于第一条线段，而另一部分等于第二条线段。

平行四边形问题

平行四边形（包括矩形、正方形、菱形）的两组对边、对角和对角线都具有某些相同性质，所以在添辅助线方法上也有共同之处，目的都是造就线段的平行、垂直，构成三角形的全等、相似，把平行四边形问题转化成常见的三角形、正方形等问题处理，其常用方法有下列几种。

方法1：连对角线或平移对角线。

方法2：过顶点作对边的垂线构造直角三角形。

方法3：连接对角线交点与一边中点，或过对角线交点作一边的平行线，构造线段平行或中位线。

方法4：连接顶点与对边上一点的线段或延长这条线段，构造三角形相似或等积三角形。

方法5：过顶点作对角线的垂线，构成线段平行或三角形全等。

梯形问题

梯形是一种特殊的四边形。它是平行四边形、三角形知识的综合，通过添加适当的辅助线将梯形问题化归为平行四边形问题或三角形问题来解决。辅助线的添加成为问题解决的桥梁，梯形中常用到的辅助线有在梯形内部平移一腰、梯形外平移一腰、梯形内平移两腰、延长两腰、过梯形上底的两端点向下底作高、平移对角线、连接梯形一顶点及一腰的中点、过一腰的中点作另一腰的平行线、作中位线等。

圆问题

在平面几何中，解决与圆有关的问题时，常常需要添加适当的辅助线，架起题设和结论间的桥梁，从而使问题化难为易，顺其自然地得到解决。

方法1：见弦作弦心距。有关弦的问题，常作其弦心距（有时还须作出相应的半径），通过垂径平分定理，来沟通题设与结论间的联系。

方法2：见直径作圆周角。在题目中若已知圆的直径，一般是作直径所对的圆周角，利用"直径所对的圆周角是直角"这一特征来证明问题。

方法3：见切线作半径。命题的条件中含有圆的切线，往往是连结过切点的半径，利用"切线与半径垂直"这一性质来证明问题。

方法4：两圆相切作公切线。对两圆相切的问题，一般是经过切点作两圆的公切线或作它们的连心线，通过公切线可以找到与圆有关的角的关系。

方法5：两圆相交作公共弦。对两圆相交的问题，通常是作出公共弦，通过公共弦既可把两圆的弦联系起来，又可以把两圆中的圆周角或圆心角联系起来。

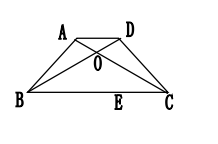图1

解：考虑过上底顶点D（或A）作对角线的平行线，把梯形问题转化为平行四边形及顶角为120°的等腰三角形问题，而解等腰三角形时，常添的辅助线是作底上的高，这样则不难求AD/BC的比值。添辅助线后的图形如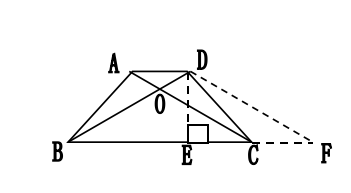图2。

图2

设DE=a，BE=EF，∠BDE=60°，∠BED=90°，可得BE=EF=

⒉聚拢集中作用：通过添置适当的辅助线，将图形中分散、远离的元素，通过变换和转化，使它们相对集中，聚拢到有关图形上来，使题设条件与结论建立逻辑关系，从而推导出要求的结论。

⒊化繁为简作用：对一类几何命题，其题设条件与结论之间在已知条件所给的图形中，其逻辑关系不明朗，通过添置适当辅助线，把复杂图形分解成简单图形，从而达到化繁为简，化难为易的目的。

⒋发挥特殊点和线的作用：在题设条件所给的图形中，对尚未直接显现出来的各元素，通过添置适当辅助线，将那些特殊点、特殊线、特殊图形性质恰当揭示出来，并充分发挥这些特殊点、线的作用，达到化难为易，导出结论的目的。

⒌构造图形的作用：对一类几何证明，常须用到某种图形，这种图形在题设条件所给的图形中却没有体现，必须添置这些图形，才能导出结论。