理想气体状态方程编辑

热力学术语

理想气体状态方程

理想气体状态方程（Ideal Gas Law），又称理想气体定律、普适气体定律，是描述理想气体在处于平衡态时，压强、体积、温度间关系的状态方程。它建立在玻义耳-马略特定律、查理定律、盖-吕萨克定律等定律的基础上，由法国科学家克拉珀龙（Benoit Pierre Emile Clapeyron）于1834年提出。理想气体状态方程可用pV=nRT表示，式中：p为压强（Pa），V为气体体积(m³)，T为温度(K)，n为气体的物质的量(mol)，R为摩尔气体常数（也叫普适气体恒量）(J/(mol.K))。

理想气体：理想气体是人们对实际气体简化而建立的一种理想模型。理想气体具有如下两个特点：①分子本身不占有体积；②分子间无相互作用力。实际应用中把温度不太低（即高温，超过物质的沸点）、压强不太高（即低压）条件下的气体可近似看作理想气体，而且温度越高、压强越低，越接近于理想气体。

具体形式

形式1：

若气体是质量为M，摩尔质量为

的理想气体，其状态方程可表示为：

式中R为普适气体常数，其取值与状态参量的单位有关，在国际单位制中R=8.31J/(mol・K)。该方程反映了一定质量气体在同一状态下三个状态参量之间的关系。

形式2：

一定质量理想气体由N个同种气体分子组成，每个气体分子的质量为m，气体的质量

，气体的摩尔质量为

，其中NA称为阿伏伽德罗常数（NA=6.02×1023/mol）。令

，n表示单位体积内的气体分子数，

，其值取为1.38×10-23J/K，称为玻尔兹曼常数。理想气体的状态方程可以进一步写为：

%20

推导过程

编辑

一般地，我们把满足气体实验定律（玻意耳-马略特定律、查理定律及盖吕萨克定律）%20和阿伏伽德罗定律（同温同压下，相同体积的任何气体含有相同的分子数）的气体称为理想气体。反映理想气体在平衡态下各状态参量之间的关系式称为理想气体状态方程。由气体实验定律可得到，一定质量的理想气体的两平衡态参量之间的关系式为：

......(1)

在标准状态

下，1mol任何气体的体积为

。因此，对

理想气体而言，由式(1)可以得出：

......(2)

由此得到理想气体状态方程:

适用条件

编辑

任何情况下都严格遵守气体实验定律的气体可以看成理想气体。同时，气体实验定律是在压强不太大(与大气压相比)、温度不太低(与室温相比)的条件下获得的，因此只要在此条件下一般气体都可以近似视作理想气体。%20

历史沿革

编辑

1834年，克拉珀龙把卡诺的思想用数学形式表达出来，最先认清了卡诺所著《论火的动力》一书的巨大科学意义。这本书实际上已经表述了热力学第二定律。克拉珀龙根据这些思想，最先把图解法引入热力学中，特别是提出P-V坐标系。1834年，导出理想气体的状态方程，这个方程后来被门捷列夫推广（门捷列夫-克拉珀龙方程）。还导出确定物质的熔点和沸点与压强之间关系的方程，即克拉珀龙-克劳修斯方程（克劳修斯于1851年论证了这个方程）。%20

修正方程

编辑

范德华方程（van%20der%20waals%20equation）是在理想气体状态方程的基础上考虑了分子间的斥力和引力而得到的半经验的修正方程。其具体形式为：

可见相比于理想气体状态方程，范德瓦尔斯方程是气体体积V的三次方程，并且多了两个参数a、b，其中参数a与分子间引力有关，参数b与分子间斥力有关，二者都与分子性质有关，对于某种确定气体来说都是常数，可由实验确定。

图1 范德瓦尔斯等温线

根据范德瓦尔斯方程可画出一组等温线，如图1所示。类似于真实气体，范德瓦尔斯等温线也存在临界点和相应的临界现象，临界温度记为TC。当T>TC时，范德瓦尔斯气体和真实气体的热力学行为类似，均可用理想气体模型进行描述。在TC时，范德瓦尔斯曲线的两端DP和QE段的行为和真实气体相同，且都是稳定相。而不同于真实气体实验时出现的气液两相共存且蒸气压不变的水平线段POQ，范德瓦尔斯等温线在此范围内却表现为弯曲线段PMONQ。其中EQ段和MP段压强与体积成反比，都是实验中可能存在的亚稳态，分别代表缺乏凝结核的过饱和蒸气和缺乏汽化核的过热液体；而MON段系统压强与体积成正比，这违背了热力学稳定条件，在实验中是无法存在的。

以理想气体模型为基础，范德瓦尔斯气体模型考虑分子间吸引和排斥力后所做的修正在一定程度上可以体现真实气体的部分性质，如临界现象等。但范德瓦尔斯等温线与真实气体等温线还有明显的区别，尤其在温度较低时，因此它只能作为研究真实气体的参考模型，还有不完善和有待改进之处。

具体应用

编辑

揭示了温度的微观本质

根据理想气体状态方程

，以及压强公式

（这里

表示分子平均平动动能）可以得到表达式：

处于同一热平衡状态的系统具有一个共同的宏观性质。称之为系统的温度。由上述推导过程可见，理想气体状态方程将气体系统的温度T这个宏观量与分子热运动平均平动动能气体

这个微观量联系了起来。温度是气体分子平均动能的量度，标志着分子无规则热运动的剧烈程度。

用于刻画平衡态示意图

实验表明，当系统处于平衡态时，描写该状态的各个状态参量之间存在一定的函数关系，我们把平衡态下，各个状态参量之间的关系式叫系统的状态方程。状态方程的具体形式是由实验来确定的。在常温常压下，实际气体都可近似地当作理想气体来处理。压强越低，温度越高，这种近似的准确度越高。

平衡状态示意图

平衡态除了由一组状态参量来表述之外，还常用状态图中的个点来表示。根据理想气体状态方程可以用于刻画气体平衡态示意图，从而分析平衡变化过程中各物理量的改变。比如对给定的理想气体，其一个平衡态可由p-V图中对应的一个点来代表（或p-T图、或V-T图中的一个点）。不同的平态对应于不同的点，一条连续曲线代表一个由平衡态组成的变化过程。曲线上的箭头表示过程进行的方向，不同曲线代表不同过程。

测量大气压

利用理想气体状态方程，巧妙地平衡了内外压差，设计出了一种较为新颖的大气压强测量方法。最大的特点在于规避了以往测量大气压强方法中的弊端，做到了实验材料绿色环保，取材方便的同时，实验过程安全易行。同时实验过程直观体现了大气压强的实际效应，实验测量的最终数值结果，满足大气压强的定性测量要求。

工业测量中的应用

①精确地测量某个异形容器容积。

根据理想气体状态方程的“在气体的质量、性质及绝对温度不变的情况下，气体的压强与体积成反比”的这个结论，提出了一个测试容积的方案：首先在一个标准容器内注入一定量经过过滤的压缩空气，测得一个压强值，再将其与被测容器联通起来，测得联通后的压强值，根据前面推导出来的结论，轻而易举地就可以计算出被测容器的容积了。

②检测成品型容器类产品的密封性问题。

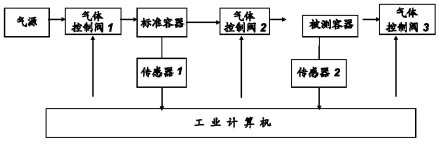检测密封性问题原理图

根据原理图，设定标准容器内的容积为V1，辅助容器的容积为V2，被测容器的容积为V3，被测工件内部的最大空间容积为V4。确定了以上各个空间的命名，首先选择一个完全无泄漏的产品作为被测容器（V4=0），并将其置于辅助容器内部。

测试开始，先由计算机向“气体控制阀1”发出接通指令，测试装置开始向标准容器的充气，当标准容器内的压强达到预定的压强值时，计算机向“气体控制阀1”发出关闭指令，关闭此阀。经过若干时间（使计算机上读到的压强数值稳定后），计算机会得到一个在标准容器内的压强值（设定为P1），此时气体的体积为V1+V2-V3。因为根据理想气体状态方程PV=nRT，可以推出P1V1=P2(V1+V2-V3) 和P2/P1=V1/ (V1+V2-V3) ，由此可以得出结论：对于一台标准的仪器（V1和V2已完全确定），测试一个完好的产品，P2/P1应该是一个定值。

理想气体状态方程

1、本站所有文本、信息、视频文件等，仅代表本站观点或作者本人观点，请网友谨慎参考使用。
2、本站信息均为作者提供和网友推荐收集整理而来，仅供学习和研究使用。
3、对任何由于使用本站内容而引起的诉讼、纠纷，本站不承担任何责任。
4、如有侵犯你版权的，请来信（邮箱:baike52199@gmail.com）指出，核实后，本站将立即删除。

下一篇布拉维点阵

上一篇拉梅常数