正割（Secant，sec）是直角三角形某个锐角的斜边与邻边的比，即正割=斜边÷角的邻边。。它的定义域不是整个实数集，值域是绝对值大于等于一的实数。它是周期函数，其最小正周期为2π。正割是三角函数的正函数（正弦、正切、正割、正矢）之一，所以在2kπ到2kπ+π/2的区间之间，函数是递增的，另外正割函数和余弦函数互为倒数。在单位圆上，正割函数位于割线上，因此将此函数命名为正割函数。和其他三角函数一样，正割函数一样可以扩展到复数。

中文名：正割

外文名：Secant

值域：绝对值大于等于一的实数

性质：周期函数

相关术语：正弦、正切、正矢

应用学科：数学

直角三角形中

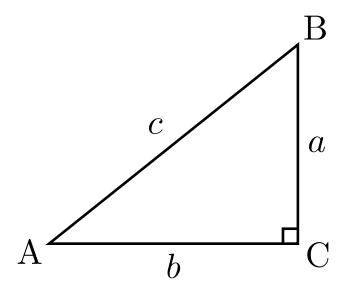直角三角形

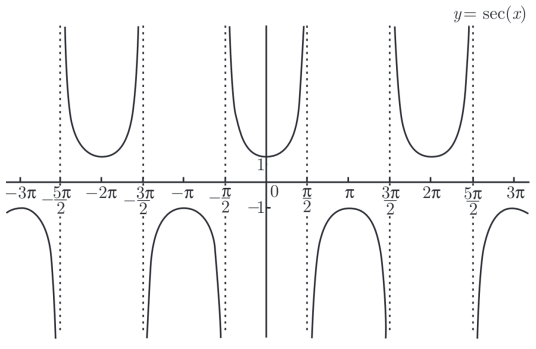
函数图像

在y=secx中，以x的任一使secx有意义的值与它对应的y值作为(x，y)。在直角坐标系中作出的图形叫正割函数的图像，也叫正割曲线。

直角坐标系中

设α是平面直角坐标系xOy中的一个象限角，

%20是P到原点O的距离，则α的正割定义为：

%20。

单位圆定义

单位圆

图像中给出了用弧度度量的某个公共角。逆时针方向的度量是正角而顺时针的度量是负角。设一个过原点的线，同 x 轴正半部分得到一个角 θ，并与单位圆相交。这个交点的 y 坐标等于 sin θ。在这个图形中的三角形确保了这个公式；半径等于斜边并有长度 1，所以有了 sec θ = 1/x 。单位圆可以被认为是通过改变邻边和对边的长度并保持斜边等于 1 查看无限数目的三角形的一种方式。

对于大于2π或小于−2π的角度，简单的继续绕单位圆旋转。在这种方式下，正割变成了周期为2π的周期函数：

%20。

对于任何角度θ和任何整数k。

级数定义

正割也能使用泰勒级数来定义:

与其他函数

正割函数和余弦函数互为倒数。

即：

%20。

微分方程定义

%20sec的微分是sec和tan的乘积

sec的导数如下：

另外

所以微分方程定义为：

指数定义

%20%20

有一些含有正割的恒等式，满足任意三角形ABC：

这些实际上是射影定理的倒数。

(1)定义域，{x|x≠kπ+π/2，k∈Z}

(2)值域，|secx|≥1。即secx≥1或secx≤－1；

(3)y=secx是偶函数，即sec(－x)=secx。图像对称于y轴；

(4)y=secx是周期函数。周期为2kπ(k∈Z，且k≠0)，最小正周期T=2π。

正割与余弦互为倒数，余割与正弦互为倒数。%20

(5)%20secθ=1/cosθ

(6)