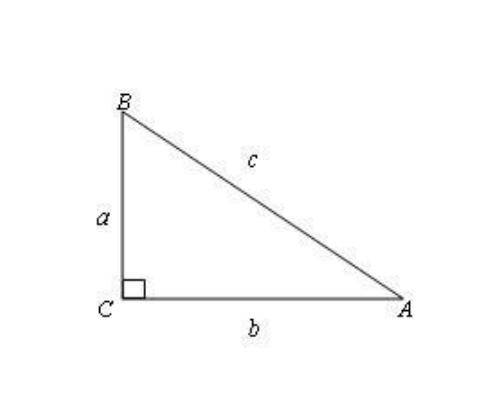
正切，数学术语，在Rt△ABC（直角三角形）中，∠C=90°，AB是∠C的对边c，BC是∠A的对边a，AC是∠B的对边b，正切函数就是tanB=b/a，即tanB=AC/BC。

中文名：正切

外文名：tangent(简写tan，旧为tg)

研究学科：数学

值域：整个实数集

定义域：{x|x≠(π/2)+kπ,k∈Z}

周期：kπ,k∈Z

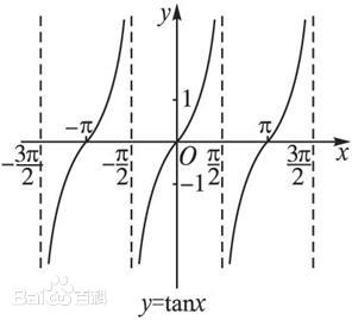
图1

由于三角函数的周期性，它并不具有单值函数意义上的反函数。

三角函数在复数中有较为重要的应用。在物理学中，三角函数也是常用的工具。

三角函数示意图

即：tanA=∠A的对边/∠A的邻边。

六种基本函数

同角三角函数

恒等变形公式

倍角公式

sin(2α)=2sinα·cosα

cos(2α)=cos^2(α)-sin^2(α)=2cos^2(α)-1=1-2sin^2(α)

tan(2α)=2tanα/

三倍角公式

sin3α=3sinα-4sin^3(α)

cos3α=4cos^3(α)-3cosα

半角公式

sin^2(α/2)=(1-cosα)/2

cos^2(α/2)=(1+cosα)/2

tan^2(α/2)=(1-cosα)/(1+cosα)

tan(α/2)=sinα/(1+cosα)=(1-cosα)/sinα

降幂公式

sin^2(α)=(1-cos(2α))/2

cos^2(α)=(1+cos(2α))/2

tan^2(α)=(1-cos(2α))/(1+cos(2α))

万能公式

sinα=2tan(α/2)/

cosα=/

tanα=2tan(α/2)/

积化和差公式

sinα·cosβ=(1/2)

cosα·sinβ=(1/2)

cosα·cosβ=(1/2)

sinα·sinβ=-(1/2)

和差化积公式

sinα+sinβ=2sincos

sinα-sinβ=2cossin

cosα+cosβ=2coscos

cosα-cosβ=-2sinsin

其他

tanA·tanB·tan(A+B)+tanA+tanB-tan(A+B)=0

高等代数中三角函数的指数表示(由泰勒级数易得)：

sinx=/(2i)

cosx=/2

tanx=/

tanA·tanB=1

值域：R

奇偶性：有，为奇函数

周期性：有

最小正周期：π

单调性：有

单调增区间：(-π/2+kπ，+π/2+kπ),k∈Z

单调减区间：无

法兰西斯·韦达(François Viète)曾在他对三角法研究的第一本著作《应用于三角形的数学法则》中提出正切定理。现代的中学课本已经甚少提及，例如由于中华人民共和国曾经对前苏联和其教育学的批判，在1966年至1977年间曾经将正切定理删除出中学数学教材。不过在没有计算机的辅助求解三角形时，这定理可比余弦定理更容易利用对数来运算投影等问题。

正切定理： (a + b) / (a - b) = tan((α+β)/2) / tan((α-β)/2)

证明 由下式开始：

由正弦定理得出

(参阅三角恒等式)

正切函数是直角三角形中，对边与邻边的比值。放在直角坐标系中（如图《定义图》所示）即 tanθ=y/x

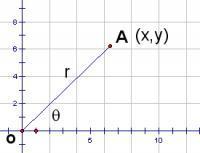定义图