-
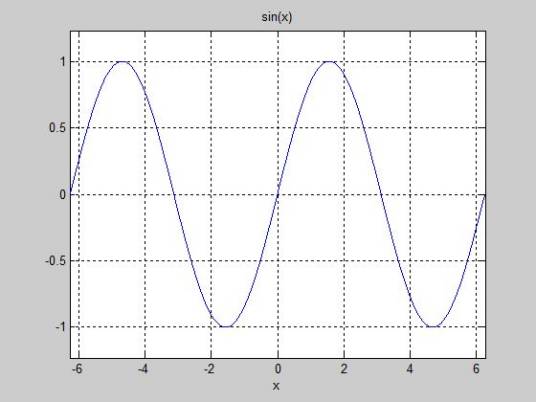
正弦 编辑
正弦(sine),数学术语,是三角函数的一种,在直角三角形中,任意一锐角∠A的对边与斜边的比,叫作∠A的正弦,记作sinA(由英语sine一词简写得来),即sinA=∠A的对边/斜边。
古代说法,正弦是股与弦的比例。
中文名:正弦
外文名:sine
所属学科:数学
属性:数学术语
定义:对边与斜边的比
古代说的“勾三股四弦五”中的“弦”,就是直角三角形中的斜边,“勾”、“股”是直角三角形的两条直角边。
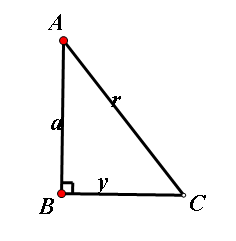 图1
图1
正弦=股长/弦长
勾、股、弦放到圆里。弦是圆周上两点连线。最大的弦是直径。把直角三角形的弦放在直径上,股就是∠A所对的弦,即正弦,勾就是余下的弦——余弦。
按现代说法,正弦是直角三角形的对边与斜边之比。
现代正弦公式:
sin = 直角三角形的对边/斜边.
如图1,斜边为r,对边为y,邻边为a。斜边r与邻边a夹角Ar的正弦sinA=y/r
无论a,y,r为何值,正弦值恒大于等于0小于等于1,即0≤sin≤1。
 sinx°函数图像
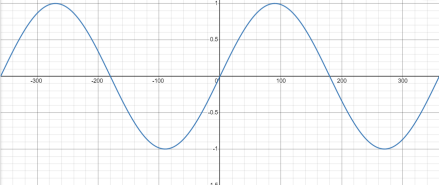
sinx°函数图像
由于三角函数的周期性,它并不具有单值函数意义上的反函数。
三角函数在复数中有较为重要的应用。在物理学中,三角函数也是常用的工具。
在RT△ABC中,如果锐角A确定,那么角A的对边与邻边的比便随之确定,这个比叫做角A的正切,记作tanA
即tanA=角A的对边/角A的邻边
同样,在RT△ABC中,如果锐角A确定,那么角A的对边与斜边的比便随之确定,这个比叫做角A的正弦,记作sinA
即sinA=角A的对边/角A的斜边
同样,在RT△ABC中,如果锐角A确定,那么角A的邻边与斜边的比便随之确定,这个比叫做角A的余弦,记作cosA
即cosA=角A的邻边/角A的斜边
一般地,在直角坐标系中,给定单位圆,对任意角α,使角α的顶点与原点重合,始边与x轴非负半轴重合,终边与单位圆交于点P(u,v),那么点P的纵坐标v叫作角α的正弦函数,记作v=sinα。通常,用x表示自变量,即x表示角的大小,用y表示函数值,这样就定义了任意角的三角函数y=sin x,它的定义域为全体实数,值域为。
表达式:f(x)=Asin(ωx+φ)
平方和关系
积的关系
sinα%20=%20tanα%20×%20cosα(即sinα%20/%20cosα%20=%20tanα)
cosα%20=%20cotα%20×%20sinα%20(即cosα%20/%20sinα%20=%20cotα)
tanα%20=%20sinα%20×%20secα%20(即%20tanα%20/%20sinα%20=%20secα)
倒数关系
tanα%20×%20cotα%20=%201
sinα%20×%20cscα%20=%201
cosα%20×%20secα%20=%201
商的关系
sinα%20/%20cosα%20=%20tanα%20=%20secα%20/%20cscα
和角公式
sin%20(%20α%20±%20β%20)%20=%20sinα%20·%20cosβ%20±%20cosα%20·%20sinβ
sin%20(%20α%20+%20β%20+%20γ%20)%20=%20sinα%20·%20cosβ%20·%20cosγ%20+%20cosα%20·%20sinβ%20·%20cosγ%20+%20cosα%20·%20cosβ%20·%20sinγ%20-%20sinα%20·%20sinβ%20·%20sinγ
cos%20(%20α%20±%20β%20)%20=%20cosα%20cosβ%20∓%20sinβ%20sinα
tan%20(%20α%20±%20β%20)%20=%20(%20tanα%20±%20tanβ%20)%20/%20(%201%20∓%20tanα%20tanβ%20)
倍角半角公式
sin%20(%202α%20)%20=%202sinα%20·%20cosα%20
sin%20(%203α%20)%20=%203sinα%20-%204sin3%20(%20α%20)%20=%204sinα%20·%20sin%20(%2060%20+%20α%20)%20sin%20(%2060%20-%20α%20)
由泰勒级数得出
sinx%20=%20%20/%20(%202i%20)
级数展开
sin%20x%20=%20x%20-%20x3%20/%203!%20+%20x5%20/%205!%20-%20...%20(%20-%201%20)%20k%20-%201%20*%20x%202%20k%20-%201%20/%20(%202k%20-%201%20)%20!%20+%20...%20(%20-%20∞%20<%20x%20<%20∞%20)
导数
(sinx)'%20=%20cosx
(cosx)'%20=%20﹣%20sinx
特定正弦函数与椭圆的关系
关于椭圆的周长等于特定的正弦曲线在一个周期内的长度的证明:
半径为r的圆柱上与一斜平面相交得到一椭圆,该斜平面与水平面的夹角为α,截取一个过椭圆短径的圆。以该圆和椭圆的某一交点为起始转过一个θ角。则椭圆上的点与圆上垂直对应的点的高度可以得到
f(c)=r%20tanα%20sin(c/r)
r:圆柱半径
α:椭圆所在面与水平面的角度
c:对应的弧长(从某一个交点起往某一个方向移动)
以上为证明简要过程,则椭圆(x*cosα)^2+y^2=r^2的周长与f(c)=r%20tanα%20sin(c/r)的正弦曲线在一个周期内的长度是相等的,而一个周期T=2πr,正好为一个圆的周长。
早在公元2世纪,正弦定理已想为古希腊天文学家托勒密(C.Ptolemy)所知。中世纪阿拉伯著名天文学家阿尔·比鲁尼(al—Birunj,973一1048)也知道该定理。但是,最早清楚地表述并证明该定理的是13世纪阿拉伯数学家和天文学家纳绥尔丁。在欧洲,犹太数学家热尔松在其《正弦、弦与弧》中陈述了该定理:“在一切三角形中,一条边与另一条边之比等于其对角的正弦之比”,但他没有给出清晰的证明。15世纪,德国数学家雷格蒙塔努斯在《论各种三角形》中给出了正弦定理,但简化了纳绥尔丁的证明。1571年,法国数学家韦达(F.Viete,1540一1603)在其《数学法则》中用新的方法证明了正弦定理。之后,德国数学家毕蒂克斯(B.Pitiscus,1561—1613)在其《三角学》中沿用韦达的方法来证明正弦定理%20。
图像中给出了用弧度度量的某个公共角。逆时针方向的度量是正角而顺时针的度量是负角。设一个过原点的线,同x轴正半部分得到一个角θ,并与单位圆相交。这个交点的y坐标等于sinθ。在这个图形中的三角形确保了这个公式;半径等于斜边并有长度1,所以有了sinθ=y/1。单位圆可以被认为是通过改变邻边和对边的长度并保持斜边等于%201%20查看无限数目的三角形的一种方式。
对于大于2π或小于−2π的角度,简单的继续绕单位圆旋转。在这种方式下,正弦变成了周期为2π的周期函数:
对于任何角度θ和任何整数k。
由于正弦的导数是余弦,余弦的导数是负的正弦,因此正弦函数满足微分方程:
这就是正弦的微分方程定义。
用其他三角函数的表示
两角和的正弦
二倍角公式
三倍角公式
半角公式
和差化积公式
万能公式
正弦函数的拉普拉斯变换为:
1、本站所有文本、信息、视频文件等,仅代表本站观点或作者本人观点,请网友谨慎参考使用。
2、本站信息均为作者提供和网友推荐收集整理而来,仅供学习和研究使用。
3、对任何由于使用本站内容而引起的诉讼、纠纷,本站不承担任何责任。
4、如有侵犯你版权的,请来信(邮箱:baike52199@gmail.com)指出,核实后,本站将立即删除。