-
有向线段 编辑
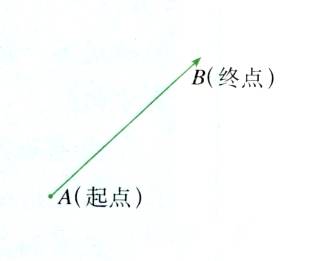
定义1 当一条线段的一个端点被指定为起点.而另一个端点被指定为终点,并且规定由起点到终点的方向叫作这条线段的方向时,那么,这种线段叫作有向线段 .
也可以简单地说,规定了起点和终点的线段叫作有向线段.或者说,规定了方向的线段叫作有向线段.起点为A,终点为B的有向线段用符号
起点与终点重合的有向线段叫作零有向线段.零有向线段的方向可以任意指定.
定义2%20如果两条有向线段方向相同.并且长度相等,就说这两条有向线段相等;规定零有向线段都是相等的%20.
必须注意,
配置在轴上的有向线段
定义3%20当一条直线的正向被指定了以后,那么.这种直线叫作轴(有向直线)%20.
若配置在轴上的有向线段的方向和轴的正向相同,那么,这种位置的有向线段叫作轴上的正方向的有向线段;若有向线段的方向和轴的正向相反,那么,这种位置的有向线段叫作轴上的负方向的有向线段.
定义4%20轴上的正方向的有向线段的长度,负方向的有向线段的长度的相反数,叫作这条有向线段的数值(代数长).规定零有向线段的数值为0%20.
有向线段
即:AB+BA=0
定理2%20(沙尔(Mishel%20Schasles)定理)%20设A,B,C是轴上的任意三点,则以下的关系式总成立,即
AB+BC=AC%20
证明%20分以下几种情形证明.
(1)B在A,C之间,并且由A到B的方向和轴的正向相同(图(a)).
由初等几何知道:∣AB∣+∣BC∣=∣AC∣(∣%20AB∣表示线段AB的长度),
而
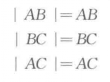 图示
图示
所以有:AB+BC=AC
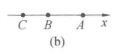
(2)B在A,C之间,并且由A到B的方向和轴的正向相反(图(b)).由(1)知道:CB+BA=CA,而由定理1知
 图示
图示
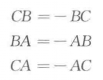 图示
图示
所以有:AB+BC=AC
其余各种情形的证明,可自己完成.
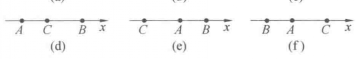 图示
图示
 图示
图示
 图示
图示
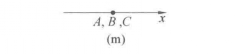 图示
图示
推论(沙尔定理的推广) 设
总成立.
1、本站所有文本、信息、视频文件等,仅代表本站观点或作者本人观点,请网友谨慎参考使用。
2、本站信息均为作者提供和网友推荐收集整理而来,仅供学习和研究使用。
3、对任何由于使用本站内容而引起的诉讼、纠纷,本站不承担任何责任。
4、如有侵犯你版权的,请来信(邮箱:baike52199@gmail.com)指出,核实后,本站将立即删除。